
Mai jos sunt câteva explicații la materialele din director. Italicized opinia mea personală, care diferă de cea general acceptată.
Pentru numerele naturale, sunt definite următoarele operații aritmetice. adunarea, scăderea, multiplicarea, diviziunea, exponentierea, extragerea rădăcinii. Nici unul dintre matematicieni nu vă va explica cum adăugarea aritmetică diferă de adăugarea algebrică. Aceleași dansuri de șamani cu tamburine. Evanghelia aritmetică începe cu adăugarea aritmetică, Evanghelia algebrică începe cu o adăugare algebrică. Acesta este nivelul științei matematice moderne.
Numerele care se adaugă sunt numite summands. Rezultatul adăugării se numește suma. Termenii se disting în ordinea scrierii lor în expresia matematică: primul termen, al doilea termen și așa mai departe. Nici un matematician nu spune că puteți adăuga numere doar cu aceleași unități de măsură. La nivelul unităților de măsură, matematicienii noștri nu au crescut încă. Nivelul lor este acele copii care, în cutia de nisip a definițiilor lor, joacă numere și nu înțeleg ce și cum fac.
Scăderea matematicii este acțiunea opusă adăugării. Numărul din care se scade este numit diminutiv. Numărul care este scăzut se numește subtrahend. Rezultatul scăderii se numește diferența. Personal, nu mi-aș clarifica inversiunea într-o acțiune matematică separată, dar am considerat-o ca un element de adăugare. Adăugarea este schimbarea cantității unității de măsură. Matematica nu are grijă dacă acest număr crește sau scade. Numai faptul de schimbare este important.
Numerele care se înmulțesc se numesc factori. Rezultatul multiplicării este numit un coeficient. Multiplicatorii, ca sumele, se disting în ordinea intrărilor din expresia matematică: primul factor, al doilea factor și așa mai departe. Care este diferența dintre înmulțire și adăugare? Atunci când se înmulțește, se schimbă unitățile de măsurare, dar când sunt adăugate, ele nu se schimbă. Pentru a emite multiplicarea pentru adăugarea multiplă este o fraudă comună. Indiferent de numărul de segmente pe care le împăturiți, nu veți obține niciodată un pătrat. De câte ori nu ați rostit cuvântul "halva", în gură nu va deveni dulce. Matematica fără unități de măsură este ca un om fără cap. Dacă studiați comportamentul omului, rupeți în prealabil capetele oamenilor, veți ajunge în mod inevitabil la concluzia că îmbrăcămintea face toate acțiunile și conduce corpuri fără viață. Aceleași rezultate sunt date de studiul numerelor fără unități de măsură. În ceea ce privește înlocuirea multiplicării prin adăugare, se arată astfel:
O diviziune este o acțiune care este inversul multiplicării. Numărul divizat se numește dividendul. Divizarea numărului se numește divizorul. Rezultatul divizării este numit un coeficient. În matematică, se presupune că împărțirea la zero este imposibilă. Diviziunea nu este o acțiune matematică. Aceasta este soluția unei probleme matematice tipice. Fracțiunile nu există, matematica lui este înlocuită de înmulțire (din nou fraudă). În intervalul de numere, împărțirea prin zero nu este deictivă, dar este în zona unităților de măsură, pe care matematica modernă o ignoră.
Exponentiation.
Multiplicarea factorilor matematici identici se numește exponentiere. Numărul care se repetă în timpul înmulțirii este baza gradului. Numărul de factori se numește exponent. Rezultatul se numește putere. Exponentierea este o altă sarcină tipică ridicată la rangul acțiunilor matematice. Matemașii spun că aceasta este înmulțirea.
Acțiunea opusă exponentierii se numește extragerea rădăcinii. Rezultatul ridicării la o putere este numit numărul rădăcinii. Exponentul se numește exponent rădăcină. Baza unui grad se numește rădăcină. O altă problemă tipică, numită acțiune matematică.
Note privind acțiunile matematice.
Acțiunile de adăugare și multiplicare au proprietățile de flexibilitate, compatibilitate și distribuție. Trebuie remarcat faptul că scăderea, divizarea, ridicarea la putere și extragerea unei rădăcini cu proprietăți similare nu există tocmai pentru că nu sunt acțiuni matematice. Proprietățile matematice ale adunării și înmulțirii trebuie îndeplinite întotdeauna și peste tot, indiferent de ramurile matematicii.
Expresii care prin definiție nu au nici un înțeles: a / 0. unde o ≠ 0 este considerată lipsită de sens, deoarece rezultatul divizării nu există; 0/0; 0 ° este considerat lipsit de sens, deoarece rezultatul acțiunilor corespunzătoare nu poate fi determinat. Așa spune ghidul matematic. Aici este necesară dezasamblarea situației în detaliu.
Matematicienii se referă la definițiile lor în același mod în care credincioșii religioși le tratează scripturile - în nici un caz nu pot fi rescrise scripturile. O astfel de abordare transformă matematica din știință în religie și matematicienii înșiși în predicatori religioși banali. Singura diferență dintre predicatorii matematicii și predicatorii religiei este că ei își scriu propriile scripturi, ceea ce le face să creadă tot restul. Ce schimbări trebuie făcute în matematică pentru a evita "expresii care nu au sens" și o repetare infinită de "nu egală cu zero"? Iată sugestiile mele.
Matematica este o regulă fără excepții. Dacă apare o excepție în regula matematică, atunci această regulă trebuie revizuită. Aceasta este o formulă universală pentru noi descoperiri matematice.
Zero nu este un număr. În sistemul pozițional de scriere a numerelor, zero înseamnă numărul unui anumit bit. Absența unui număr nu poate fi un număr. Introducerea acestei reguli în matematică, matematicienii nu trebuie să precizeze în mod constant că numărul nu este egal cu zero în această expresie matematică.
Unitățile de măsură sunt aceleași elemente ale matematicii ca și numerele. Unitățile de măsură dau tuturor acțiunilor matematice un înțeles care nu poate fi văzut, având în vedere numai numerele. Zero este absența unității de măsură în cauză.
Împărțirea cu zero apare nu în zona numerelor, ci în zona unităților de măsură. În sistemul de poziționare a numerelor de scriere, zero înseamnă nici un număr de o anumită cifră. Absența unui număr nu poate fi un număr. Introducerea acestei reguli în matematică, matematicienii nu trebuie să precizeze în mod constant că numărul nu este egal cu zero în această expresie matematică. Acesta este modul în care regulile de divizare arata ca zero.
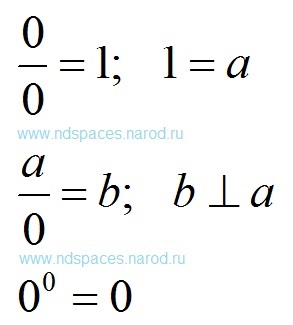
Zero împărțită la zero este egală cu unitatea de măsură. Această regulă vă permite să introduceți orice unitate de măsură. De-a lungul istoriei, omenirea a folosit întotdeauna această regulă, introducând o varietate de unități de măsură diferite pentru o varietate de lucruri. În acest caz, toate unitățile de măsurare inventate au fost supuse regulilor matematice generale.
Unitatea de măsură împărțită la zero este egală cu unitatea perpendiculară de măsură. În matematică, există o regulă: orice număr înmulțit cu zero este egal cu zero. Este logic să presupunem că atunci când numărul este împărțit la zero, toate numerele vor apărea simultan. Toate numerele sunt combinate cu o unitate de măsură. Deoarece numărul dividendelor are deja o unitate de măsură proprie, noua unitate de măsură nu poate fi decât perpendiculară pe o unitate de măsură deja existentă. Această regulă de divizare cu zero se extinde numai la unitățile de măsurare actuale care există în natură. Unitățile de măsură virtuale, inventate de noi, nu respectă această regulă. Nu vă puteți imagina dolari perpendiculare, piese, ori și așa mai departe.
Puterea de la zero până la zero este egală cu zero. Dacă nu se ridică nimic în nici un fel, rezultatul va fi absent. Absența rezultatului este de obicei marcată cu numărul "zero".
De câte ori se va multiplica 0 cu 15? - Dacă 0 este înmulțit cu 15, atunci se obține 0.
0 * 15 = 0
3 înmulțiți cu zero - 3 multiplicați cu zero egal cu zero.
3 * 0 = 0
Numărul împărțit la 0. - Profesorii trebuie să răspundă că numărul nu poate fi împărțit la zero, deoarece rezultatul nu există.
Înmulțirea și împărțirea cu 0. - Înmulțirea cu 0 orice număr duce la 0, divizarea cu 0 este imposibilă.
Ce se întâmplă atunci când ne înmulțim cu zero? - Rezultatul este zero.
Câți vor fi doi la primul grad? - Două în primul grad sunt egale cu două.
Cum arată un număr natural? - Numărul natural pare foarte frumos. Fără coadă (partea fracționată), fără coarne (exponent), fără abdomen (semn minus). În prima fotografie toate numerele sunt naturale, puteți admira.
Înmulțirea cu zero - În multiplicare cu zero, nu este nimic interesant - ca rezultat, zero este întotdeauna obținut.
Regulile pentru matematică, în cazul în care un număr este înmulțit cu zero, care este zero. - Așa-i, îți amintești bine. Câți ani au trecut de când ați învățat această regulă?
Divinosta opt la șapte. "Dacă împărțiți nouăzeci și opt de șapte, primiți paisprezece."
98: 7 = 14
2 pătrat este de patru.
2 2 = 2 * 2 = 4
3 pătrat este de nouă.
3 2 = 3 * 3 = 9
12 în piață este o sută patruzeci și patru.
12² = 144
Două până la a patra putere este șaisprezece. Nu am o insignă de gradul patru, așa că vă voi da un exemplu cu multiplicare.
2 * 2 * 2 * 2 = 16
Pătratul cu numărul 81 este de șase mii cinci sute șaizeci și unu.
81² = 6561
Dacă sunteți interesat, pătratul a ce număr este 81, atunci acesta este de nouă.
9² = 81
Tabela de componente în diviziune - Prima imagine are un astfel de tabel. Componentele din diviziune sunt dividende, divizoare, coeficienți.
Construirea numerelor în pătrat - Pentru a ridica numerele într-un pătrat, trebuie să multiplicați numărul cu exact același număr. Iată exemple.
2 2 = 2 * 2 = 4
3 2 = 3 * 3 = 9
11 ² = 11 * 11 = 121
0: a = 0. Deși aceasta nu mai este "Evanghelia aritmetică", ci "Evanghelia algebrei". Acum nu este Evul Mediu și matematicienii care nu mă vor arde la miză. Sper că da.
0: a = 0
Care sunt numerele naturale? - Nu există numere naturale, doar numerele sunt naturale. Figurile sunt simple simboluri grafice, prin intermediul cărora scriem numere. Definiția numerelor naturale poate fi găsită în imaginea din partea de sus a paginii.