Fig. 2. Entropia condiționată
3. Entropia comună - cantitatea medie de informație per pereche de simboluri transmise și primite (Figura 3).
H (X, Y) = H (Y, X) = H (X) + H (Y / X) X × Y).
4. entropia mutuală este entropia aspectului comun al mesajelor dependente de statistică (figura 4).
Fig. 3 entropie comună
Fig. 4. entropia mutuală
În practică, există adesea simboluri și mesaje interdependente. De exemplu, atunci când trimiteți mesaje text sunt transmise nu numai litere, și cuvinte care au anumite semnificații. În acest caz, fiecare literă și o combinație de litere au probabilități diferite de apariție în text. Entropia condiționată ia în considerare relația evenimentelor prin probabilitățile lor condiționate.
Luați în considerare circuitul din Fig. 5:
Fig. 5. Mesagerie
Sursa mesajelor X - generează mesaje ale căror elemente sunt caracterele alfabetului sursă. probabilitatea apariției la ieșirea cărora este egală cu p (x1), p (x2). p (xm), în timp ce:
Entropia sursei este incertitudinea apariției simbolului alfabetului primar la ieșirea sursei mesajului și este determinată de relația:
()
Receptorul de mesaje Y - primește mesaje ale căror elemente sunt simbolurile alfabetului receptorului. probabilitatea apariției la intrarea cărora este egală cu p (y1), p (y2). p (ym), în timp ce:
Entropia receptorului este incertitudinea apariției la intrarea receptorului a mesajelor de simbol după ce apare la sursa de ieșire și este determinată de relația:
Dacă nu există pierderi de informații în canalul de comunicații (fără interferențe, fără erori etc.), atunci simbolul yi corespunde simbolului xi. În caz contrar xi poate fi considerat ca oricare dintre posibilitățile y1, y2. ym. cu probabilități corespunzătoare.
În absența pierderilor: H (X) = H (Y). În prezența interferențelor, ele distrug unele informații. În acest caz, pierderea informațiilor poate fi determinată printr-o entropie condiționată particulară și generală.
Este convenabil să se calculeze entropia condițională generală prin intermediul matricelor de canal (matricea stărilor de tranziție).
Pierderea informațiilor din canal poate fi estimată de la sursă sau de la receptorul mesajului.
Luați în considerare ordinea de determinare a pierderilor din partea sursei (semnalul transmis este cunoscut). În acest caz, probabilitatea condiționată p (yj / xi) înseamnă probabilitatea ca mesajul yj să fie recepționat când mesajul xi este transmis. Matricea canalului are forma prezentată în Tabelul. 1.
Probabilitatea localizării pe diagonală caracterizează probabilitatea unei transmiteri corecte, restul fiind fals. Pentru semnalele echiprobabile la intrarea receptorului, entropia condițională totală se calculează cu formula:
Pentru semnalele non-echiprobabile la intrarea receptorului, entropia condițională totală se calculează cu formula:
O entropie condiționată specială care determină pierderile atribuite semnalului y1. este egal cu:
Exemplul 1. Se calculează entropia sursei mesajelor care produce două simboluri 0 și 1 cu probabilități p (0) = 3/4, p () = 1/4 și probabilități condiționale: p (0/0) = 2/3, p (/ 0) = 1/3, p (0/1) = 1, p (/ 1) = 0. că este, după 1 există întotdeauna 0.
Soluție: Pentru cazul elementelor interdependente, care nu sunt echilibrate, entropia este:

Exemplul 2. Determina entropia sursei de mesaj, dacă probabilitățile apariției simbolurilor la intrarea receptorului sunt: P (b1) = 0,1; P (b2) = 0,3; P (b3) = 0,4, P (b4) = 0,2 iar matricea canalului are forma:
Suma probabilității în aceleași condiții este
Soluție: definiți entropia sursei
.
= 0,1 x 0,01 + 0,3 x 0,98 + 0,4 x 0,01 + 0, x 2 x 0,01 = 0,301;
0,1 x 0 + 0,3 x 0 + 0,4 x 0,98 + 0,2 x 0,02 = 0,396;
0,1 x 0 + 0,3 x 0 + 0,4 x 0,01 + 0,2 x 0,97 = 0,198;
Entropia sursei este:
Exemplul 3. Pentru a determina sursa entropiei și mesajele transmise de entropie condiționate prin canalul de comunicație, și care constă din simboluri echiprobabile, dacă efectul interferenței descris în matricea canalului:
.
Soluție: Pentru caracterele echiprobabile dintr-un mesaj, entropia sursei mesajului este:
Entropia condiționată totală este:
=
Exemplul 4. Determina entropia receptorului de mesaje dacă probabilitatea apariției simbolurilor a1, a2 și a3 la intrarea sursei de mesaj este P (a1) = 0,5; P (a2) = 0,3 și P (a3) = 0,2, iar matricea canalului are forma:
,
Soluție: entropia receptorului este:
.
Probabilitatea apariției simbolurilor la intrarea receptorului
;
;
.
.
2. ENTROPIA SURSĂ A MESAJELOR CONTINUALE
Pentru a descrie proprietățile informaționale ale unei surse continue (semnal), se folosește conceptul de entropie diferențială. Pentru a obține acest lucru, vom folosi formula pentru entropia mesajelor discrete. În conformitate cu graficul funcției de densitate a probabilității (figura 6), putem scrie p (xi) =?. Unde p (xi) este probabilitatea ca x să se situeze în etapa i-a de cuantizare.
Fig. 6. Graficul funcției de densitate a probabilității
În acest caz, expresia pentru entropie poate fi reprezentată în formă
Trecem la limită:
.
entropia totală Sursa de informații continuu este format din doi termeni, unul dintre care este determinat de legea de distribuție, iar a doua este o constantă care determină pasul de cuantizare, care afectează precizia de măsurare. Acest termen al expresiei definește o componentă constantă și este exclus din considerație.
Valoarea primului termen este determinată de legea distribuției și caracterizează entropia diferențială a sursei continue (deoarece f (x) este densitatea de probabilitate sau legea distribuției diferențiale)
Entropia diferențială face parte din entropia sursei mesajelor continue, care depinde de densitatea de probabilitate a semnalului x (t). emise de sursă.
Clasele diferite de fenomene fizice și procese se supun legilor de distribuție diferite. Semnalele continue sunt caracterizate complet prin legi de distribuție (integrale sau diferențiale). Orice semnale reale sunt supuse anumitor restricții, de exemplu: puterea medie (echipamentul de încălzire); puterea instantanee sau vârf (suprasarcină).
Deoarece entropia diferențială depinde de densitatea de probabilitate, determinăm pentru ce lege este maximă. Adică, la ce distribuție de probabilități, semnalul unei anumite puteri are entropia maximă. Pentru a găsi valoarea maximă a entropiei, este necesar să se folosească teorema variată cu utilizarea multiplicatorilor Lagrange incertați în condițiile de normalizare și invarianța pătrații medii:
; .
Rezolvând ecuațiile, obținem o lege simetrică normală de distribuție
Dacă puterea medie nu este limitată
atunci obținem o lege uniformă de distribuție.
Definim entropia diferențială pentru o distribuție normală, adică pentru un semnal cu o putere medie limitată. Distribuția normală obținută ca rezultat al rezolvării problemei variaționale este simetrică. Dacă înlocuim x = y-mx în integrale pentru entropia diferențială. atunci integralele nu se schimbă și, prin urmare, entropia nu depinde de așteptările matematice și este egală cu entropia variabilei centrale aleatoare.
Definiți valoarea maximă pentru entropie:
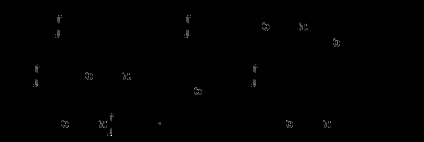
Entropia diferențială pentru o distribuție normală este:
Entropia totală pentru o distribuție normală este:
Dacă luăm în considerare faptul că h (x) este așteptarea matematică a funcției [-log2 f (x)] dintr-o variabilă aleatoare x cu densitatea f (x), atunci putem scrie.

În conformitate cu teorema limitei centrale, legile de distribuție normală fac obiectul unei clase largi de așa-numite procese aleatorii Gauss sau semnale reale.
Zgomot alb - interferența cu cele mai multe proprietăți „maligne“, adică transmite cantitatea maximă de informații dăunătoare pentru o putere medie dată, și simplifică calculele pentru cel mai rau caz ....
Pentru ca un semnal cu putere de vârf limitată să aibă informativitate maximă, este necesar ca acesta să aibă o distribuție uniformă (figura 9). Definim entropia diferențială pentru o distribuție uniformă, adică un semnal cu o putere de vârf limitată. Dacă puterea P-vârf, atunci - amplitudinea maximă. Ecuația pentru entropia diferențială cu toleranță pentru constrângeri are forma:
Entropia diferențială pentru o distribuție uniformă este:
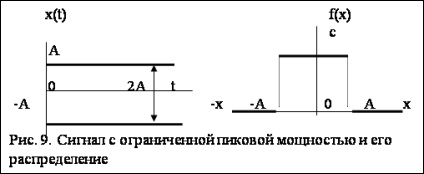
Entropia totală a unui semnal cu o distribuție uniformă este:
unde m este numărul de nivele de cuantificare.
Definim entropia diferențială pentru distribuția exponențială. Această distribuție este utilizată pe scară largă pentru a determina intensitatea defecțiunilor echipamentelor radio electronice
Entropia totală pentru distribuția exponențială este:
2. Yaglom AM Yaglom IM Probabilitate și informații. M. 1957.
3. Shannon K. Lucrează pe teoria informațiilor și a ciberneticii. - M. Ed. străine. Literatura. 1963. - 830 p.
4. Wolkenstein, entropia și informația despre MV. - M. Nauka, 1986. - 192 p.
5. Tsymbal VP Teoria și codificarea informațiilor. - M. Vysshcha Shkola, 1977. - 288 p.
6. Metode probabile în tehnologia informatică. / Ed. AN Lebedev, E.A. Chernyavsky. -M. Învățământul superior săpt. 1986.
7. Sedov E.A. Interrelația informației, a energiei și a entropiei fizice în procesele de gestionare și de auto-organizare. Informare și management. M. Nauka, 1986.