În această secțiune, luăm în considerare formula referitoare la integralele duble și curbilinii.
. integramentul se numește integral pe un contur închis.
Vom numi direcția pozitivă a parcurgeri contur închis simplu, care, la care partea cea mai apropiată de observator zona delimitată de bucla este situată la stânga observatorului.
Să presupunem că u. t.e.nepreryvny la (D) și T închis contur neted pe porțiuni, apoi au formula:
,care se numește formula verde.
Pentru derivarea calculului integral va fi redus cu curba închisă integralei zona delimitată din interiorul curbei.
Am împărțit producția în mai multe puncte:
1) Domeniul D este un trapez curbilinar:
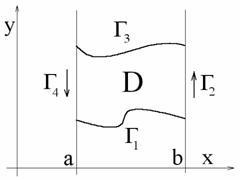
Acum scriem integralul pe contur în formă. și integrala dublă va arăta astfel:
- se dovedește prima parte a egalității.
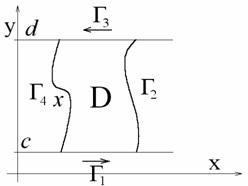
Acum scriem integralele secțiunilor individuale ale curbei și integralele lui Γ2 și Γ4 sunt egale cu zero:
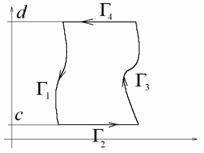
Noi scriem integralul dublu în formă
. în consecință, am dovedit acest lucru. dar mai devreme am dovedit și asta. prin urmare, pot fi reprezentate ca.
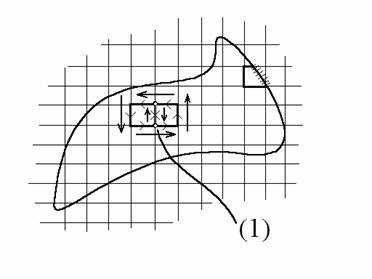
Integrala peste granița dintre cele două elemente (1) este zero, deoarece este evaluată de două ori în direcții opuse, prin urmare, suma tuturor integralelor liniei va fi egală cu integrala peste graniță D.
Considerăm acum câteva corolări ale formulei lui Green.
Condiții pentru independența integrala curbilinii
din calea integrării într-o simplă legătură
zona din avion
Următoarele patru condiții sunt condițiile de echivalență:
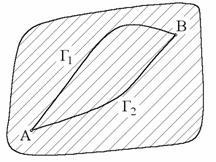
1) (curbele Γ1 și Γ2 au aceeași origine - punctul A și același punct final B)
2) pentru orice curbă închisă netedă Γ.