Cu privire la originea geometriei (orașul Lobachevsky).
În unele bibliografii este descrisă și cea de-a treia foaie de diagrame geometrice. Dar, în același timp, în textul faimoasei lucrări a lui Lobachevsky, sunt descrise doar 17 figuri plasate pe 2 mese pliabile. În / în coperta epocii, cu o ștanțare șubredă pe coloana vertebrală. Se păstrează coperțile de publicare pentru piesa XXV. Format: 21x13 cm Raritate!





4. Harrison D. Horblit. O sută de ani. New York, 1964, nr. 69a.
5. M. Kline. Gândire matematică din timpurile antice la cele moderne. New York, 1972, p. 873-81.
6. Dicționarul biografic al figurilor științei și tehnologiei. Moscova, 1959. T. 1, pp. 524-527.
7. Dicționarul biografiei științifice (faimosul DSB), vol. VIII, New York, 1973, p. 428-434.
8. Bolkhovitinov V. Buyanov A. Zakharchenko V. Ostroumov G. Povestiri despre campionatul rus. Sub ediția generală a lui V. Orlov. Moscova, ed. "Garda Tânără", tipografia Red Flag, 1950, pp. 47-51.
9. Oamenii din știința rusă. Eseuri privind cifrele remarcabile în știință și tehnologie. T.1, Moscova-Leningrad, OGIZ, 1948, pp. 90-98.
"Gloria neterminată a lui Lobacovski este că el a rezolvat o problemă care a rămas nerezolvată de două mii de ani". S. Lee.
- Pentru păcatele noastre. - a murmurat colegul Nikolski și a privit cu înverșunare la Nikolai Ivanovici. În forma lui Lobachevsky, acum părea să fie ceva satanic. Aici, Nikolai Ivanovici se opri la tablă, un zîmbet ciudat, strălucitor, rătăcind peste buze. Își coborî sprâncenele ascuțite, își trase capul blond întunecat aproape de ochi, își înclină capul. Merită, protejând desenul cu spatele lui și, uitându-te în jur cu ochii uimiți, spune:
-. Principala concluzie la care am venit cu presupunerea de linii, în funcție de unghiul, permite existența geometriei într-un sens larg, mai degrabă decât ca ne-a oferit cu o ipotecă. În acest spațiu, am dat un nume științific al geometriei imaginare, în cazul în care un caz special include geometria și utilizate în mod obișnuit, cu restricția în poziția generală a măsurătorii necesare, de fapt. Care este esența, semnificația ascunsă a geometriei non-euclideene descoperită de Lobachevsky? De ce a numit marele geometru imaginarul ei? De ce este geometria euclidiană un caz particular sau, mai exact, limitator, al geometriei lui Lobachevsky? geometrie Do Lobachevsky este real în sensul respectării spațiului fizic, dacă există o suprafață la care noua geometrie este corectă, sau dacă fructe inutil de imaginație, ficțiune tihnit, fantezie, dovada formală a independenței cincilea postulat de celelalte axiome euclidiene? Care dintre cele două geometrii descrie lumea reală cu o precizie mai mare? Pas cu pas, am urmărit modul în care Lobachevsky sa apropiat de deschiderea noului geometrie, urmat în măsura în care este posibil să vorbim despre intimă, cea mai bună lucrare a geniului minții, în cazul în care haosul de observații trecătoare pe baza experienței și intuiției născut adevăr fără precedent, treptat, cristalizeaza sub forma unei clare formulă. Prima descoperire importantă Lobachevsky a fost de a demonstra independența cincilea postulat al geometriei euclidiene din celelalte prevederi ale acestei geometrii. Cea de-a doua descoperire a fost sistemul consistent logic al noii geometrii. El și-a privit geometria exact ca o teorie, și nu ca o ipoteză. A ajuns la concluzia logică că în spațiul mondial și, eventual, în. microcosmos, suma unghiurilor unui triunghi trebuie să fie mai mică de două unghiuri drepte, Lobachevsky îndrăzneală a prezentat axiomă inițială, un postulat, și a construit o geometrie neobișnuită precum și euclidiană, lipsit de contradicții interne. El a numit imaginarul nu pentru că a considerat-o o construcție formală, ci pentru că era încă disponibilă doar imaginației, nu experienței. Nu a lăsat din nou gândul să se întoarcă la măsurarea triunghiurilor cosmice și să stabilească adevărul. Fara a schimba nimic în geometrie „absolut“, a înlocuit doar a cincea antipostulatom postulat, antievklidovoy axiomă: prin punctul desemnat poate deține o multitudine de drept, nu trece asta. În desen arata astfel:
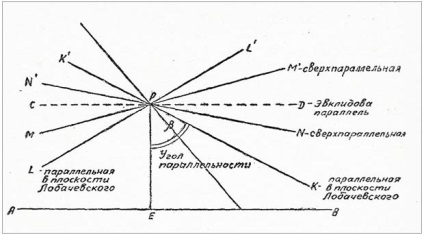
Lobachevski a schimbat foarte înțelegerea liniilor paralele. În Euclid disjuncte și paralele - același lucru, în Lobachevsky: (. A se vedea desenul), toate care nu se intersectează linia dat AB, doar două linii sunt numite paralele - l K1RK. și LRL1. Toate celelalte care se află în fascicul dintre cele paralele nu sunt considerate ca atare (în literatura modernă se numește superparallel). Prin urmare, postulează precizează că în cazul dat linie dreaptă AB, și nu se află pe punctul P ei, prin punctul P în planul AVR poate fi tras două linii drepte paralele cu o anumită linie dreaptă AB. Paralel Lobachevski, prin urmare, cheamă pe aceia care separă intersectarea de linia intersectată AB. Distanța dintre linia AB și fiecare dintre liniile paralele nu rămâne constantă - scade spre paralelism și crește în direcția opusă. Liniile paralele se pot apropia unul de altul, dar nu pot trece. Planul în care există astfel de linii paralele este numit, de obicei, avionul Lobachevsky. Acest plan nu este „plat“ în euclidiană smysle.V plan euclidiană unghiul paralel este neschimbat și este întotdeauna egală cu 90 °; În geometria lui Lobachevsky el poate lua toate valorile - de la 0 la 90 °. În consecință, geometria euclidiană este un caz particular (limitator) al geometriei lui Lobachevsky, în care unghiul paralelismului este variabil. Din punct de vedere geometric, magnitudinea unghiului de paralelism depinde de lungimea X a PE perpendiculară; adică dacă perpendicularul scade, unghiul paralel crește, apropiindu-se treptat de 90 °. Foarte condiționată în desen, aceasta poate fi reprezentată după cum urmează:
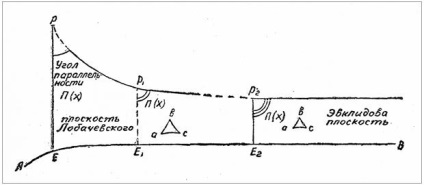
Cu alte cuvinte, atunci când punctul P tinde să coincidă cu punctul E, adică, atunci când X tinde la zero, dacă unghiul de paralelism tinde la 90 °. Astfel, în noua geometrie există o interdependență între unghi și segment. Când unghiul de paralelism este drept, adică 90 °, interdependența dispare. În geometria euclidiană nu există nici una. În non-euclidian reprezintă cel mai important moment. Din această interdependență, se deduce formula de bază a întregii geometrii Lobachevski. În formula Lobachevski introduce așa-numita constantă liniară. În știința modernă, constanta liniară este raza de curbură a spațiului Lobachevsky; Valoarea constantei depinde de conditiile fizice specifice intr-o anumita parte a spatiului mondial. Valoarea excepțional mare arată constant că spațiul nostru are o mare raza de curbură, și, prin urmare, destul de mici, aproape de zero curbură, adică, spațiul în partea noastră a universului este caracterul plat, euclidian. Dar dacă presupunem că o constantă liniară poate avea valori diferite, atunci fiecare dintre aceste valori va avea o geometrie proprie, specială. În consecință, poate exista un număr infinit de geometrii diferite. Pentru Kant, spațiul este o entitate nemodificată; pentru Lobachevsky - este o formă de existență a materiei. Spațiul se poate schimba cu materia. Da, da, Lobachevsky a creat o geometrie ciudată. Nu există astfel de cifre; suma unghiurilor unui triunghi este întotdeauna mai mică de două linii și, pe măsură ce crește triunghiul, tinde la zero. Încercați să vă imaginați un triunghi a cărui sumă de unghiuri este egală cu nimic! Și în această geometrie uimitoare nu pot exista triunghiuri cu o suprafață arbitrar de mare. Există o relație directă între unghiurile și lungimile laturilor triunghiului, care nu este în Euclid. Nu există dreptunghiuri. Relațiile pentru cerc sunt, de asemenea, diferite. Planul și spațiul Lobachevski au o curbură negativă constantă etc. "Newton este cel mai mare geniu și cel mai fericit dintre toate, deoarece sistemul lumii este doar unul și ar putea fi deschis doar o singură dată", a spus Lagrange. Respingând conceptele newtoniene de spațiu și timp, Lobachevsky a creat o lume nouă - un imens „Lobachevsky pace“, în care familiar pentru noi lumea lui Euclid este doar un caz de limitare a regiunii infinit de mic spațiu în care ne târască ca furnicile. Această parte infinitezimală a spațiului conține toate bucuriile, speranțele, tragediile, trecutul și prezentul nostru, întreaga semnificație a existenței noastre.
-. Este imposibil să nu se implice în opinia lui Laplace - suna vocea groasă Lobachevskian - că stelele pe care le vedem aparțin singura reuniune a corpurilor cerești, cum ar fi cei care văd cât de puțin pete sclipitoare în constelațiile Orion, Andromeda, Capricorn și altele. Deci, ca să nu mai vorbim de faptul că în spațiul imaginației poate fi continuat pe termen nelimitat, natura însăși ne arată o astfel de distanță, față de care dispar chiar micimea și distanța de teren noastre la stelele fixe. Părul se mișca pe capul lui Nikolsky. Se încrucișă și murmură:
"Pentru păcatele noastre, Domnul are milă".
Faptul este că în St. Petersburg a trăit un alt matematician Lobachevsky, o rudă îndepărtată a lui Nikolai Ivanovici. Acest Petersburg Lobachevsky, Ivan Vasilievich, a fost obsedat de ideea de a tăia cercul și a plictisit Ostrogradsky. În tabelul de la Ostrogradskii se află lucrarea lui Ivan Vasilyevici "Programul geometric care conține cheia cadranului lunetului inegal (3: 4) (1: 4) și un segment în compoziția jumătății diferenței dintre acestea situate". După ce a dezvăluit memoarul "Cu privire la originea geometriei" al Kazanului Lobachevsky, Ostrogradski a fost îngrozit. Ce nonsens. Acest Lobachevsky nu are suficientă cvadratură a cercului, acum el este angajat în teoria paralelismului! A inventat o nouă geometrie - imaginară. E greu să te descurci cu oamenii nebuni. Mikhail Vasilievici a scris într-un cuvânt: "Acest Lobachevsky nu este un matematician rău, dar dacă trebuie să-i arăți o ureche, el o arată din spate și nu din față". Fuss a explicat cu amabilitate Academicianului Ostrogradski că acest Lobachevsky nu era deloc Lobachevsky, ci rectorul Universității din Kazan.
"Atunci este o altă chestiune", a spus Mikhail Vasilyevich și a scris:
„Este posibil să se autodepăși și a citit memoriile sredaktirovanny rău, dacă timpul de cheltuieli să fie valorificată cunoașterea noilor adevăruri, dar este mai dificil de descifrat manuscrisul, pe care nu le conține și care este dificil de idei nu înalte și circulația bizară de propuneri, neajunsuri în raționamentul și în mod deliberat excentricități aplicate. Această ultimă caracteristică este inerentă în manuscrisul domnului Lobachevski. Ni se pare că memoriul lui Lobachevsky despre convergența seriei nu merită aprobarea Academiei ".
- Îți aduc aminte de tine.
"E mai bine!" A spus Musin-Pușkin.
Lista operelor lui Lobachevsky:
1. 1823. Geometria. A fost publicată în 1909 de Societatea fizico-matematică din Kazan. La "Geometrie" sunt anexate două dovezi ale postulatului Euclidului, pe care Lobachevsky le-a expus în prelegerile sale din 1815-17.
6. 1834. Scăderea gradului într-o ecuație pe termen lung, atunci când indicele fără unitate este împărțit la 8 ("Notes of Scientists", 1834, I, pp. 3-32).
7. 1834. Cu privire la dispariția liniilor trigonometrice ("Notes of Scientists", 1834, II, pp. 167-226).
9. 1835. Geometria imaginară ("Notes of Scientists", 1835, I, pp. 3-83, tabelul din Figurile 1-8). Aproape coincide cu numărul 13. Reprinse în Lucrările complete ale lucrărilor colectate, vol. I, pp. 71-120.
10. 1835. Modul de a asigura dispariția liniilor infinite și de a aborda valoarea funcțiilor de la un număr foarte mare ("Notes Scientists Notes", 1835, II, pp. 211-342).
11. 1835-1838. Noua geometrie începând cu teoria paralelă completă ( "Oameni de stiinta Note", 1835, III, pp 3-48 Introducere și Capitolul I, tabelul I, Figura 1-20, 1836, II, pp 3-98, Capitolul IІ -..... V, tabelul 3, Figurile 21-41, 42-60, 61-75, .. 1836, III, paginile 3-50, capitolul VI-VII, Figurile 76-91 Tabelul 2, 92-106; ... 1837 I p 3-97, capitolul VIII-XI, Tabelul 2 fIG 107-120, 121-134;. ... 1838, I, pp 3-124, capitolul XII ;. 1838 III, paginile 3-65, capitolul XIII. ). Reprinted în lucrările complete ale lucrărilor colectate, vol. I, p. 219-486.
12. 1836. Aplicarea geometriei imaginare la anumite integrale ("Notes Scientists", 1836, I, pp. 3-166, 1 tabel, Figurile 1-20). Reprinted în colecția completă de lucrări, vol I, pp. 121-218.
13. 1837. Géométrie imaginaire par M.-r. N. Lobatschewsky, rector al Universității de Cazan. (Journal of Creleet, T. 17, tet.4, pp. 295-320, 1 din Tabelul 1-8, Berlin, 1837, trimis în 1834 sau 1835). Repetat în ansamblul complet este compus. II, pp. 581-613.
16. 1842. Cu privire la probabilitatea des résultats moyens, tirés des observations répétées. (Par dl Lobatschefsky, recteur de l'Universite de CAZAN. Jurnal der Reinen und angewandten Mathematik von GRELLE. Bd. 24. Heft. 2, pp. 164-170). Traducerea unor pagini din capitolul XII al Noilor Începeri. Works Complete, pp. 428-438.
18. 1845. O analiză detaliată a raționamentului prezentat de M. Popov sub titlul: "Cu privire la integrarea ecuațiilor diferențiale ale hidrodinamicii reduse la o formă liniară", pe gradul de Doctor în Matematică și Astronomie. Anexă la teza de doctorat a lui Popov. Kazan, 1845.
19 1852. Semnificația anumitor integrali definiți ("Notes of Scientists", 1852, vol. IV, vol. I, pp. 1-26, issue II, pp. 27-34). Această lucrare a apărut în limba germană, publicată de GA Erman "Archiv für wissenschaftliche Kunde von Russland". Berlin 1855. Bd. 14, pp. 232-272, cu titlul: "Ueber den Werth einiger bestimmten Integrale. Nach dem Russischen von Herrn Lobatschefskji, prof. Emer. în Kasan.
20. 1856. Pangéométrie ou Precis de géométrie fondée sur une Theorie générale et des rigoureuse parallèles, par N. Lobatscheffsky, professeur émérite de l'Université de Kasan et de l'honoraire Membre Université de Moscou (articole științifice primite scrise de un profesor de Kazan Imperial Universitatea, pentru a comemora cincizeci de ani de existență, adică. I. Kazan. 1856, pp. 279-340. Republicat în lucrări complete, vol. II, p. 617-680).
21. 1855. Panganometrie, profesor onorific N.I. Novgorod ( "Note științifice" 1855, că eu, pp 1-56; .. Kazan, 1856 La fel ca și numărul 20. retipărit în lucrări complete, că eu, pagina 489-550 ..).