Atunci când sunt expuse la aparat radio electronic (un filtru, un amplificator, o întârziere de linie, și altele). Curent sinusoidala-TION sau reacția de tensiune, adică. E. Variația mărimilor electrice la ieșire gura-roystva poate fi determinată folosind un complex de soluții UI-Toda ecuații Kirchhoff . Impulsul și secvența impulsurilor nu sunt oscilații electrice sinusoidale. Cu toate acestea, se știe că oscilația non-sinusoidal pfu lu-periodic u (t) poate fi extins într-o serie trigonometric infinit (seria Fourier) compusă din constantă și sinusoidal co-stavlyayuschih (armonice) având diferite amplitudine, frecvență și fază. Un astfel de set de armonici se numește spectru. În acest caz, se disting spectrul de amplitudine și spectrul de fază.
Spectrul de amplitudine al unei secvențe periodice de impulsuri dreptunghiulare este prezentat în Fig. 9,5, a.
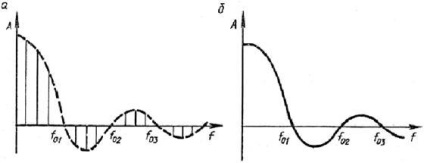
Fig. 9.5. Spectrele de frecvență ale unei secvențe periodice de impulsuri dreptunghiulare (a) și un singur impuls dreptunghiular (b)
Fiecare armonic este prezentat separat lungimea liniei Koto roi proporțională cu amplitudinea armonicei și Raspaud pozițiile în raport cu axa de frecvență este determinată de fază. Acest spectru este numit condus. Plicul spectrului liniar al amplitudinilor variază în conformitate cu legea sin x / x. Frecvențele f01. F02. ... depind de durata impulsului și sunt determinate de expresia f0m = m / tι (m = 1, 2, 3). Numărul de armonici cuprins între frecvențele 0, f01. F02. ... este egal cu raportul puls. Prin urmare, atunci când retras, perioada de repetiție chenii T spectru amplitudine Mill vitsya mai "dens", și este transformată în întregime pe termen (fig. 9.5, b) la T → ∞.
Spectrul de fază sau spectrul de fază de frecvență se numește setul de faze ale componentelor armonice. Având în vedere fazele inițiale, amplitudinile armonicelor pot fi fie pozitive, fie negative, luate în considerare în Fig. 9,5, a. Într-o serie de cazuri, suntem interesați doar de spectrul de amplitudine (frecvență-amplitudine) fără a lua în considerare fazele. În acest caz, spectrul de frecvență de amplitudine (figura 9.5, a) va arăta așa cum se arată în Fig. 9.6.
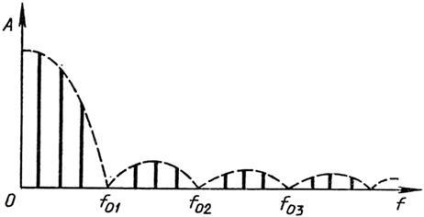
Fig. 9.6. Spectrul de spectru de amplitudine al secvenței periodice a impulsurilor dreptunghiulare
Pentru a forma de impulsuri de ieșire, atunci când trece prin circuitul (sau dispozitiv) nu este diferită de forma impulsului de intrare, este necesar ca acest circuit trece toate armonici, păstrând fazele inițiale ale acestora. Numărul de armonici transmiși de circuitul electric (sau dispozitivul) determină lățimea de bandă # 916; F. În consecință, în cazul ideal, banda de trecere trebuie să fie infinit de mare. Având în vedere Fig. 9.6, se poate observa că armonicile cu cele mai mari amplitudini sunt concentrate în banda de frecvență 0. f01. Prin urmare, forma impulsurilor este determinată în cea mai mare măsură de armonicile acestui domeniu special. Pentru a trece aceste armonici, lățimea de bandă a circuitului electric (dispozitiv) trebuie să fie egală cu # 916; F = f01 = 1 / tu. Pentru a crește abrupta frontală și cutoff a impulsurilor, lățimea de bandă este mărită la valoare F = (2 ... 3) / t și