1) Prima acțiune. Rezultatul unui minus dintr-o matrice (introducerea unui minus într-o matrice).
Luăm un minus dincolo de matrice, schimbând de la fiecare element al semnului matricei:
Introducem un minus în matrice, schimbând semnul fiecărui element matriceal.
2) A doua acțiune. Înmulțirea unei matrice cu un număr.
Singurul lucru care este de dorit în acest exemplu este de a adăuga un minus la matricea: Dar dacă toate elementele matricei au fost împărțite la 7 fără restul. atunci este posibil (și necesar!) să fie divizat.
3) A treia acțiune. Transformați matricea.
Apoi rescriim a doua linie din a doua coloană:
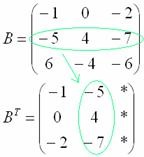
4) A patra acțiune. Suma (diferența) matricelor.
NU TOATE MATRIXELE SUNT FOLOSITE. Pentru a efectua adunarea (scăderea) matricelor, este necesar ca acestea să aibă aceeași dimensiune.
A cincia acțiune. Înmulțirea matricelor
Pentru ca o matrice să fie înmulțită cu o matrice, este necesar ca numărul de coloane ale matricei să fie egal cu numărul de rânduri ale matricei.
- Încercați să prindeți imediat legea.
Multiplicați matricea prin matrice
Vă rugăm să rețineți că! Este aproape întotdeauna așa!
Astfel, atunci când se înmulțește, nu puteți rearanja matricile!
Determinanți, proprietăți, complemente algebrice, calcule
Desemnări. Dacă este dată o matrice. atunci se determină determinantul său. De asemenea, foarte des, determinantul este notat cu o latină sau cu o greacă.
Deci, determinantul "trei la trei" este redus la soluția a trei determinanți mici, sau așa cum sunt numiți, MINOR. Termenul pe care recomand să-l amintesc este, de altfel, memorabil: minorul este mic.
Deoarece metoda de extindere a determinantului de către prima linie este aleasă. este evident că totul se învârte în jurul lui:
1) Scriem semnul corespunzător din matricea semnelor:
2) Apoi notăm elementul însuși:
3) SEMNAT, ștergem rândul și coloana în care se află primul element:
Cele patru numere rămase formează un determinant de doi-doi, care se numește MINOR al acestui element (unități).
Trecem la al doilea element al liniei.
4) Scriem semnul corespunzător din matricea semnelor:
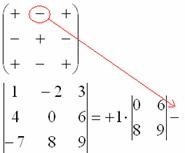
5) Apoi scrieți al doilea element:
6) SENSIBIL, ștergem rândul și coloana în care se află al doilea element:
Celelalte patru numere sunt scrise într-un mic identificator.
Cel de-al treilea element al primei linii. Fără originalitate:
7) Scriem semnul corespunzător din matricea semnelor:
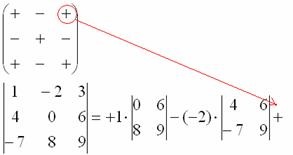
8) Se scrie cel de-al treilea element:
9) SENSIBIL, ștergem rândul și coloana în care se află al treilea element:
1. Determinantul este mai profitabil să se deschidă pe linia TOI (coloana), unde:
Din care urmează un fapt important: rândurile și coloanele determinantului sunt egale.
2. Dacă două rânduri (sau două coloane) ale determinantului sunt schimbate,
atunci semnul schimbărilor determinante
Adică orice rearanjare a perechilor de rânduri (coloane) implică o schimbare a semnului determinantului la cel opus.
3. Din rândul (coloana) determinantului, se poate face un factor comun
Opusul este, de asemenea, adevărat: multiplicatorul nu poate fi efectuat doar, ci și introdus. și, pe oricare linie sau în orice coloană a determinantului.
4. Dacă două rânduri (coloane) ale determinantului sunt proporționale
(ca un caz special - același lucru), atunci acest determinant este zero
Determinantul cu rândul zero (coloana) este zero
Ce proprietăți ale factorilor determinanți sunt utile să știm?
1) Valoarea determinantului nu se modifică în timpul transpunerii. Proprietatea este memorată.
2) Orice permutare pe perechi a rândurilor (coloane) modifică semnul determinantului la cel opus. De asemenea, ne amintim de proprietate și încercăm să nu o folosim pentru a evita confuzia.
3) Din rândul (coloana) determinantului, puteți lua multiplicatorul (și îl puteți întoarce). Noi o folosim acolo unde este profitabilă.
Dacă rândurile (coloanele) determinantului sunt proporționale, atunci este zero. Determinantul cu rândul zero (coloana) este zero.
Sistemul de ecuații liniare Teorema lui Cramer
Sisteme de înregistrare a ecuațiilor liniare în formă de matrice