Rezumat: Sunt studiate cele mai simple formule de cvadratură ale tipului de interpolare-dreptunghiuri, trapezoizi, Simpsons. Pentru a estima eroarea reală a formulelor, regula lui Runge este utilizată. Este dată conceptul de formule de cvadratură Gaussiană. Sunt luate în considerare metode de calcul al integraliilor multidimensionale.
În această prelegere vom examina problema integrării numerice. Formulele pentru integrarea numerică a funcțiilor unei variabile se numesc formule de cvadratură. Problema calculului aproximativ al unui integrat definit (pe un interval sau într-un domeniu multidimensional) este de fapt împărțită în două subtasme independente. Prima este integrarea unei funcții tabulare (obținută, de exemplu, într-un experiment de laborator). În acest caz, nu există informații a priori despre netezirea integranței, iar posibilitățile de selectare a nodurilor de integrare sunt foarte limitate. Pentru această problemă, formulele de tip quadrature ale tipului de interpolare și regulile Runge de estimare a erorilor vor fi cele mai eficiente.
A doua sarcină este de a calcula valoarea unui integral definit dintr-o funcție cunoscută. În acest caz, operațiunea cu cea mai mare intensitate a resurselor din punct de vedere al calculului este calculul valorii funcției. Este de dorit să construiți o metodă numerică care vă permite să obțineți cea mai mare precizie posibilă cu cel mai mic număr de calcule, în timp ce alegerea nodurilor formulelor de cvadratură este în întregime în mâinile calculatorului. În acest caz, cele mai eficiente sunt formulele de tip quadrature de tip Gauss.
7.1. Formulele de tip quadrature ale tipului de interpolare (formule Newton-Cotes)
Cea mai simplă formulă de cvadratură (formula de integrare numerică) poate fi obținută după cum urmează. Să fie necesar să se calculeze integralele
Să presupunem că f (t) nu se modifică () în intervalul [a, b] în considerare. Apoi Dacă
atunci obținem formula de dreptunghiuri cu un punct central
Desigur, constantele pentru formula de mai sus sunt exacte - spune construit formula de cuadratură vor fi corecte la polinoame grad poate fi 0. Este ușor de demonstrat că formula cu punctul central al dreptunghiurile va da o valoare exactă în cazul unei funcții liniare. Pentru toate celelalte funcții, această formulă va fi considerată ca o formulă aproximativă.
Presupunând că funcția f (t) în intervalul de integrare [a, b] este suficient de aproape liniar, este posibil să se înlocuiască valoarea aproximativă a zonei i integrantă a unui trapez cu o înălțime (b - a) și bazele f (a) și f (b). Apoi se obține formula trapezoidală
În general, formulele de cvadratură sunt obținute prin integrarea polinomului de interpolare care aproximează integradul. Familia formulelor de cvadratură obținute în acest fel se numește formule de tip de interpolare (formula Newton-Cotes).
Introducem o grilă pe intervalul de integrare, definind valorile funcției la nodurile rețelei. Nodurile vor fi denumite noduri ale formulei de cvadratură (sau cvadratură). Să presupunem, ca și în problema interpolare, că există un set de noduri. Să lăsăm și tabelul [tk. tk + 1] va fi uneori numit un segment elementar.
Înlocuim integradul prin polinomul său de interpolare sub formă de Lagrange. Vom presupune asta
Să luăm în considerare câteva cazuri particulare.
Formula trapezelor. Pe intervalul [tk. tk + 1] înlocuim integradul printr-un polinom de interpolare de gradul I:
după care, după integrarea peste intervalul elementar, obținem o valoare aproximativă a integrului pe [tk. tk + 1]:
După însumarea integralelor peste toate intervalele elementare [tk. tk + 1] obținem formula trapezului pentru intervalul [a, b]:
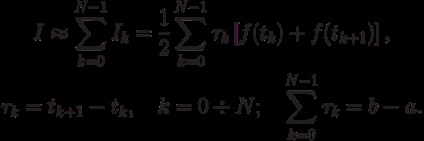
Pe o rețea uniformă (grilă cu noduri echidistant) cu formula rezultată ia forma