O cantitate este numită aleatoare dacă își ia valorile în funcție de rezultatele unui anumit test (experiență) și pentru fiecare rezultat elementar are o singură valoare. O variabilă aleatoare este numită discretă. dacă setul tuturor valorilor posibile ale acestuia este finit.
Din punct de vedere geometric, mulțimea tuturor valorilor posibile ale CB discret reprezintă un sistem finit de puncte pe axa numerică.
Fie X un CB discret. ale căror valori posibile și singure posibile sunt numerele x1. x2. ..., xn.
probabilitatea acestor valori (adică, pi este probabilitatea evenimentului că X ia valoarea xi) /
Evenimentele X = xi (i = 1, 2, ..., n) formează, în mod evident, un grup complet de evenimente
Corespondența dintre toate valorile posibile ale unui CB discret și probabilitățile acestora se numește legea distribuției unui CB dat.
Pentru un SV discret, legea distribuției este dată de tabel
Prima linie conține toate valorile posibile ale CB, iar cea de-a doua - probabilitățile lor.
O variabilă aleatoare X va fi numită continuă dacă toate valorile posibile completează complet un anumit interval finit sau infinit 
Pentru a caracteriza CB X, funcția de distribuție
dacă numărul de valori pe care funcția de distribuție le ia este numărabil, atunci X este un CB discret în cazul în care CB infinit-continuu.
Proprietățile funcției de distribuție:
4) dacă x1
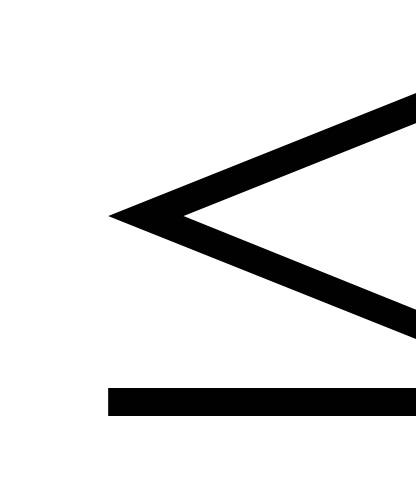
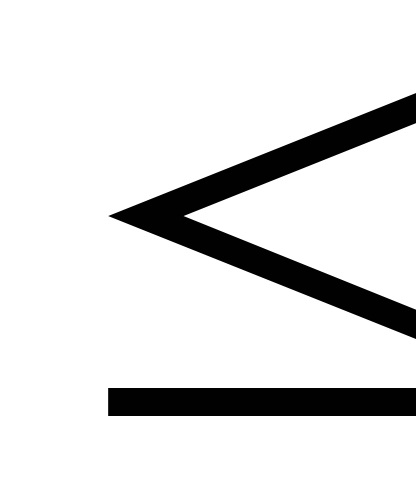
5) P (x1
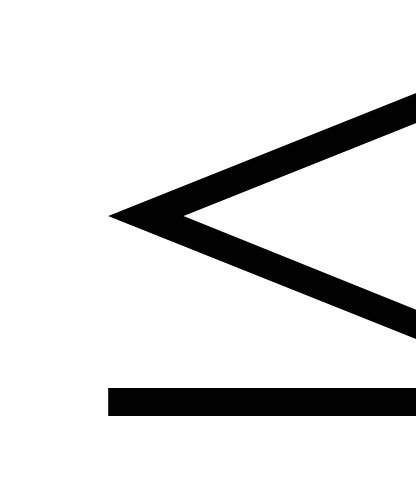
Să presupunem că pentru o CBX continuă funcția de distribuție Ф (х) are un derivat continuu
f (x) se numește densitatea de probabilitate (pentru o distribuție dată) sau legea distribuției diferențiale CB X.
Secvențe de numere pseudo-aleatoare
Numerele aleatoare și pseudo-aleatoare, numere care pot fi considerate ca implementarea unor variabile aleatoare. De obicei, ne referim la implementarea unei variabile aleatoare, uniform distribuit în intervalul (0,1), sau în apropierea unor astfel de implementări având un număr finit de cifre în reprezentarea sa. Cu o interpretare atât de îngustă, un număr aleator (dp) poate fi definit ca un număr compus din cifre aleatoare (sf). S. c. o p radix -ary este rezultatul unui experiment cu un număr de rezultate la fel de probabile (fiecare rezultat corespunde unuia dintre un număr de cifre). Experimente pentru a obține fiecare s. c. se presupune că sunt independente.
O sursă de la. c. Inițial, rezultatele recensământului populației și alte tabele de numere obținute experimental. Primele mese din. c. au fost compilate în 1927 în legătură cu nevoile statisticilor matematice (nevoia de selecție aleatorie în planificarea experimentului). Ulterior, în legătură cu apariția metodei de testare statistică s-au creat dispozitive experimentale speciale - senzori sau generatori c. h. bazate în majoritatea cazurilor pe utilizarea zgomotului de dispozitive electronice.
Odată cu dezvoltarea metodei testelor statistice este, de asemenea, concepte legate apariției numerelor pseudoaleatoare (p. H.). Ultimul poate fi obținut prin calcul în raport cu o formulă predeterminată (algoritm), dar proprietățile lor trebuie să fie apropiate de cele ale p. h. Cele mai frecvente algoritmi în care fiecare număr următor este calculat din cel precedent. Secvențele obținute în acest mod au o perioadă care le distinge în esență de secvențele c. h. Algoritmi obține n. h. Mai insuficient studiată, dar este dată metoda de calcul statistic preferință testul n. h. t. k. proprietăți ale secvenței n. h. Testul poate fi investigată prin intermediul unor calcule și dispozitive experimentale furnizează nouă secvență. h. cu fiecare utilizare.
Random este o cantitate dintr-o anumită gamă, probabilitatea apariției acesteia fiind determinată de funcția legii distribuției. Exemplu: distribuția uniformă a unei variabile aleatorii discrete în intervalul 1-6 - probabilitatea este 1/6.
Obținerea unei valori cu adevărat aleatoare este posibilă numai dacă se utilizează un mecanism fizic sau chimic ca mecanism de conducere. Cu ajutorul unui calculator, pot fi obținute secvențe pseudo-aleatoare. Pentru ei este caracteristic faptul că alegerea acelorași valori inițiale conduce la generarea de secvențe identice și există un N astfel încât termenul N + 1 este egal cu primul termen al secvenței.
În C, există funcții care vă permit să generați o secvență de numere întregi pseudo-aleatoare, setați valoarea inițială a secvenței, setați valoarea aleatorie inițială (în funcție de timpul sistemului).
Apoi, sunt luate în considerare metode de generare a numerelor pseudo-aleatoare.
6.1. Metoda de pătrate medii
a) Se alege un numar arbitrar de 2k cifre x0. care este pătrat, rezultatul este un număr de 4 cifre, din care sunt selectate numerele medii de 2k, care formează următorul număr aleatoriu. Procedura se repetă de câte ori este necesar.
b) Se iau două numere arbitrare de 2k, care se înmulțesc și se completează cu o valoare de 4k. Din mijloc, sunt luate 2k cifre, următorul număr este obținut de la produsul obținut și cel precedent.
Numerele rezultate pot fi considerate pseudo-aleatoare, deoarece semnele de mijloc depind de cele extreme care sunt aruncate.
6.2. Metoda multiplicativă
Sunt date constantele C și m. Se ia un număr arbitrar, următorul număr pseudo-aleator este numărul curent, înmulțit cu C împărțit la modulul.
6.3. Metoda aditivului (generator Fibonacci)
Se definește întregul m. Sunt luate două numere întregi. Următorul număr este egal cu suma celor două precedente, luate modulo.
6.4. Metodă liniară
Este definit de un set de numere întregi [j], j [1, k] și întreg m. Inițial, toate numerele sunt luate. Următorul număr pseudo-aleator este egal cu suma peste 1 din modulul productions [j] xi + 1-j divizat.
6.5. Metoda combinată
Luăm un număr întreg numit x0 x 2. Număr de
x0 'este ultimul 2k al pătratului x0,
x0 "este primul 2k din produsul lui Cx0 '(C este un număr întreg),
x0 '' 'sunt primele cifre de 2k ale pătratului x0' ',
x0 '' '' sunt ultimele cifre de 2k ale pătratului x0 '' '
Calitatea generatorului de secvențe pseudo-aleatoare poate fi determinată prin construirea unei histograme a numerelor pseudorandomului. legea distribuției este uniformă, înălțimea coloanelor ar trebui să fie aproximativ aceeași.