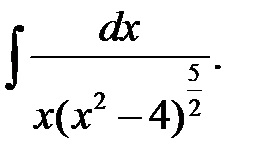1). Dacă rădăcinile din interand au forma, etc. unde n, m, q, p, s, r, etc. sunt numere naturale, atunci ea este transformată într-o fracțiune rațională prin substituire. unde k este cel mai mic multiplu comun al exponenților rădăcină u.
2). Dacă rădăcinile din interand au forma, etc. n, m, q, p, s, r și așa mai departe. sunt numere naturale, atunci ea este transformată într-o fracțiune rațională prin substituire. unde k este cel mai puțin comun multiplu al exponenților rădăcini și
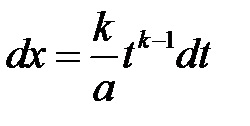
3). Dacă rădăcinile din integrand au forma
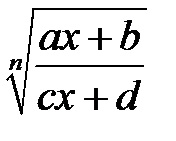
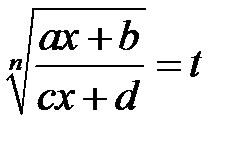
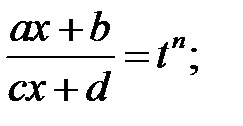
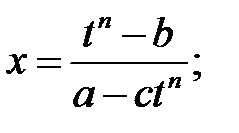
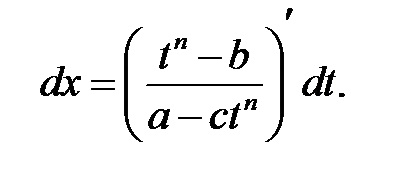
Exemplu: Găsiți integralele: a)
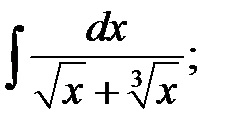
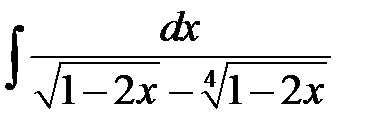
Remarcă A) În integrand există rădăcini ale puterilor a doua și a treia a lui x, așa că facem substituția x = t 6. unde 6 este cel mai mic multiplu comun al numerelor 2 și 3.
7.2. Integrarea iraționalităților prin intermediul permutărilor trigonometrice. Integralele speciilor după selecția sub semnul radical al întregului pătrat și utilizarea substituției liniare
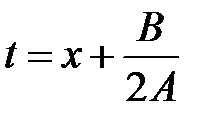
1. integralitatea formularului; substituție
Exemplu: Găsiți un integrator nedefinit.
Pentru a scăpa de radical, folosim o substituție și facem o substituție în integralitatea nedeterminată
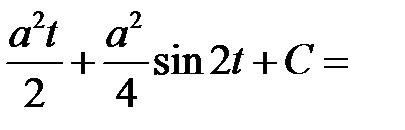
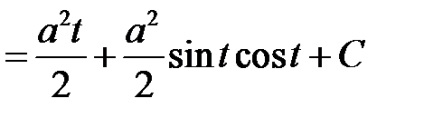
2. integralitatea formularului;
Exemplu: Găsiți integralul nedefinit
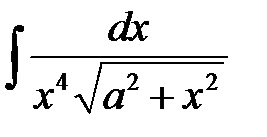
Remediu Cu ajutorul substituției, reducem integralitatea funcției iraționale la rațional în ceea ce privește păcatul t.
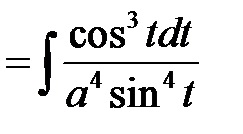
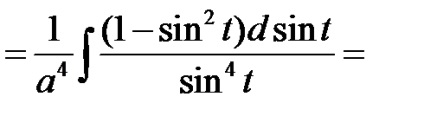
=
3. integralitatea formularului;
Exemplu: Găsiți integralul nedefinit