Acest post este inspirat de această sarcină.
Se pare că multe articole interesante și site-urile întregi sunt dedicate stelelor, poligoanelor de stele și polyhedra.
Ceea ce vedeți este luat din acest minunat site: zvzd3d.ru/. Și aceasta este doar o mică parte. Ce nu există!
Dar mai întâi vom trata cu stele plate.
În Wikipedia, despre stele se spune:
O stea este un anumit tip de poligoane plate neconvexe, care, cu toate acestea, nu are o definiție matematică unică. De obicei sub stele înseamnă cifre asemănătoare cu forma unei stele.
Și imediat după aceasta, sunt date două definiții.
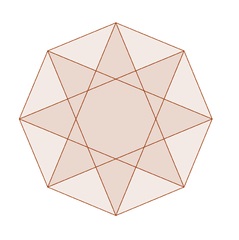
Steaua corectă cu 8 vertexuri inscripționată în 8-gonii obișnuiți
Definiția 2. Un poligon în formă de stea
Fiecare vârf al unui n-poligon obișnuit este conectat cu m-a de la el pe cerc în sensul acelor de ceasornic. Steaua obținută în acest fel este desemnată ca. În acest caz, punctele de intersecție dintre laturi nu sunt considerate ca fiind noduri. O astfel de stea are n noduri și n laturi, precum și un n-gon obișnuit. Este de asemenea numit un poligon în formă de stea și este o formă în formă de stea a n-gonului corespunzător.


O stea cu cinci puncte înscrisă în pentagonul obișnuit și în Pentagramul lui Penrose
Stars poate fi conectat (poligoanele uniforme Nonseparated) nu fiind compuși alt poligon regulat sau stelată sau pot fi deconectate. degradând în mai multe poligoane identice sau stele conectate.
Set discret de stele în două dimensiuni
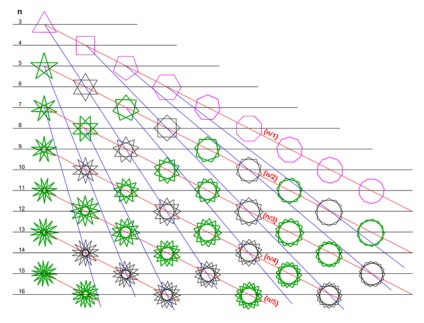
Purple - poligoane convexe.
Verdele legate de stele (unde n și m sunt numere relativ prime).
Negre - stele ne-conectate (unde n și m nu sunt numere relativ prime).
Liniile albastre conecta poligon (convex sau stea conectat) nu este conectat cu toate stelele, este compusul (după turn) un număr diferit de poligoane identice, cum ar fi aceasta.




Un polyhedron în formă de stea (corp în formă de stea) este un polyhedron neconvex, ale cărui fețe se intersectează reciproc. Ca și în polyhedra ne-stelare, fețele sunt unite în perechi în coaste, în timp ce liniile interne de intersecție nu sunt considerate coaste.
Forma stea a unui polyhedron este un poliedron obținut prin extinderea fețelor unui poliedru dat prin marginile lor la următoarea intersecție cu alte fețe de-a lungul unor noi margini.
Poliedrele stelare corecte sunt polyhedra stele, ale căror fețe sunt aceleași poligoane obișnuite sau în formă de stea. Cauchy a constatat că există doar 4 corp stelat drept nu este un compus al organismelor platonice și stelate, organisme numite Kepler - Poinsot: toate forma 3 stelat unui dodecaedru, și unul dintre forma stelată a unui icosahedron. Celelalte polidre cu stea regulate sunt fie compuși de solide platonice, fie compuși ai corpurilor Kepler-Poinsot.
Multe forme de stele polyhedra sunt determinate de natura însăși. De exemplu, fulgii de zăpadă sunt proeminențe plane ale polyhedra stelare. Unele molecule au structuri regulate de cifre tridimensionale.
Polidrurile polidrece poligrafice sunt polyhedra de stele, ale căror fețe sunt poligoane regulate sau în formă de stea, dar nu neapărat aceleași. În acest caz, structura tuturor vârfurilor trebuie să fie aceeași (starea de omogenitate). Coxeter și alții, până în 1954, enumeră 53 de astfel de organisme și au prezentat o ipoteză cu privire la caracterul complet al listei lor. Numai mult mai târziu a fost posibil să se demonstreze că lista de polyhedra obținută de ei este cu adevărat completă.
poliedre uniforme - poliedre convexe regulate și semiregulate (solide platonice si arhimedice) si poliedre semiregulate stelat dreapta împreună numit poliedre omogen. Aceste organisme sunt toate fețele poligoane regulate (convexe sau stelate), dar vârfurile sunt aceleași (adică, acolo de transformare ortogonală un poliedru care transforma orice nod la oricare alta). Exista exact 75 polyhedra omogene.
Dau o legătură într-un articol din Wikipedia, pentru că am adus doar o mică parte din imagini și o mică parte din informație!
Star polyhedra
Mai multe link-uri.
1. Poligoane în formă de stea în formă de stea dorigami.narod.ru/dorigami_rco.html
2. Pentagrama Wikipedia
3. Hexagram Wikipedia
4. Wikipedia Octagramul
5. Site-ul polyhedrons.ru