unde xi valoarea reală -I -lea a variabilei timpului Bi-lea, ax'i valoarea prezisă -lea -i variabilei timpul Bi-lea, N - numărul de proiecții.
Conform rezultatelor obținute pe foaia "Simple Sk. medie „registru de lucru“ LR6.Primer 1.Stanki.xls „(vezi. Figura 56), o medie mobilă timp de trei luni, are o valoare egală cu ILW 12,67 (celula D16), în timp ce pentru valoarea medie se deplasează de 4 luni CAO este 15 , 59 (celula F16). Apoi, este posibil să se ipoteza că utilizarea unor cantități mai mari de date statistice se agravează, mai degrabă decât îmbunătățește acuratețea estimărilor, prin mutarea medie.
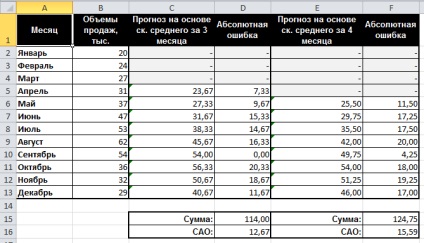
Figura 56. Exemplul 1 - Rezultatele predictiilor medii simple
În grafic (vezi Figura 57), construit din rezultatele observațiilor și previziunilor cu un interval de 3 luni, puteți vedea o serie de caracteristici comune tuturor aplicațiilor metodei cu mișcare medie.
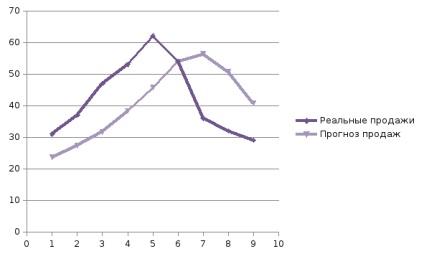
Figura 57. Exemplul 1 - graficul curbei prognozate prin metoda simplă a mediei mobile și programul real de vânzări
Valoarea prognozată obținută prin metoda simplă a mediei mobile este întotdeauna mai mică decât valoarea reală dacă datele inițiale cresc în mod monoton și sunt mai mari decât valoarea reală dacă datele originale scad monoton. Prin urmare, dacă datele cresc sau scad monoton, atunci folosind o medie simplă, nu puteți obține previziuni exacte. Această metodă este cea mai potrivită pentru datele cu deviații aleatorii mici de la o valoare constantă sau variabilă lentă.
Principalul dezavantaj al metodei simplei medii mobile se datorează faptului că, atunci când se calculează valoarea estimată, cea mai recentă observație are aceeași greutate (adică semnificație) ca cea precedentă. Acest lucru se datorează faptului că ponderea tuturor observațiilor recente N implicate în calculul mediei mobile este 1 / N. Atribuirea greutății egale contravine ideii intuitive că, în multe cazuri, cele mai recente date pot spune mai multe despre ce se va întâmpla în viitorul apropiat decât cele precedente.
Media mobilă ponderată. Contribuția diferitelor puncte de timp poate fi luată în considerare prin introducerea unei greutăți pentru fiecare valoare a exponentului în intervalul de alunecare. Rezultatul este o metodă medie ponderată ponderată, care poate fi scrisă matematic ca:
unde este greutatea cu care se utilizează indicatorul atunci când se calculează.
Greutatea este întotdeauna un număr pozitiv. În cazul în care toate greutățile sunt aceleași, metoda de mișcare simplă medie degenerează.
Acum, marketerul poate folosi metoda medie ponderată ponderată timp de 3 luni. Dar mai întâi trebuie să înțelegeți cum să alegeți greutățile. Utilizând instrumentul Find Solution, puteți determina greutatea optimă a nodurilor. Pentru a determina greutatea nodurilor utilizând instrumentul Find Solution, în care abaterea medie medie este minimă, urmați acești pași:
Alegeți Instrumente -> Găsiți soluția.
În caseta de dialog Căutarea soluției, setați celula țintă G16 (vedeți foaia "Greutăți"), minimizând-o.
Celulele variabile specifică domeniul B1: B3.
Setați constrângerile B4 = 1.0; B1: B3 ≥ 0; B1: B3 ≤ 1; B1 ≤ B2 și B2 ≤ B3.
Porniți căutarea soluției (rezultatul va fi afișat).
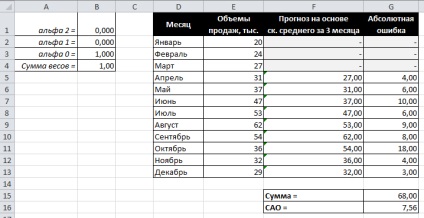
Figura 58. Exemplul 1 - rezultatul căutării greutăților valorilor indicatorilor atunci când se folosește metoda medie ponderată ponderată
Rezultatele obținute arată că distribuția optimă a greutăților este astfel încât întreaga greutate este concentrată pe cea mai recentă observație, în timp ce deviația medie medie este egală cu 7,56 (vezi și Figura 59). Acest rezultat confirmă ipoteza că observațiile ulterioare ar trebui să aibă mai multă pondere.
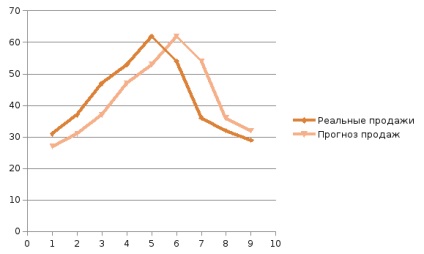
Figura 59. Exemplul 1 - graficul curbei prognozate prin metoda medie ponderată ponderată și programul real de vânzări