Dependența pericolului de eșec la timp poate fi în mod evident de trei tipuri:
1. Pericolul de defectare cu creșterea timpului de funcționare scade.
Elementul îmbunătățește fiabilitatea în funcționare. Acest caz rar are loc, de exemplu, în procesul de derulare preliminară, atunci când în perioada inițială de funcționare elementele defecte, defecte sunt înlocuite cu altele noi. Lotul de elemente astfel format îmbunătățește caracteristicile lor de fiabilitate.
2. Pericolul de defectare cu creșterea duratei de funcționare crește. Elementul își degradează caracteristicile de fiabilitate în timpul funcționării. Elementul "devine vechi". Acesta este un caz evident, cel mai comun.
3. Pericolul de defecțiuni în timpul funcționării nu se modifică, rămâne constant. Elementul aflat în funcțiune "nu devine vechi", rămâne "nou". Evident, acesta este un fel de model teoretic.
Să luăm în considerare acest ultim caz în detaliu. În cazul în care # 955; (t) = const, apoi în conformitate cu (1.10) obținem
Legea rezultată a fiabilității se numește exponențială și are o mare importanță în teoria fiabilității. Rata de eșec în conformitate cu punctul (1.3) este egală cu
Timpul mediu dintre eșecuri conform (1.11) este
Se calculează probabilitatea funcționării fiabile în intervalul egal cu timpul mediu de defect t = T0.
Fiabilitatea este foarte mică, doar aproximativ o treime din elemente vor rămâne operaționale. Prin urmare, pentru elementele responsabile, timpul de operare ar trebui ales cu mult mai puțin decât durata medie de viață a elementului (t < iar probabilitatea de eșec este aproximativ egală cu Probabilitatea de eșec într-un interval de timp mic # T este elementul care poate fi folosit # 955; # 8710; Această probabilitate nu depinde de timpul lucrat, dacă elementul este solid, atunci comportamentul său ulterior nu depinde de istoria trecutului. Converse este, de asemenea, adevărat. Pentru modelele de defecțiuni, atunci când istoricul nu afectează comportamentul eșecurilor, legea exponențială de fiabilitate este valabilă. Astfel de modele de defecțiuni sunt denumite scheme de daune instantanee.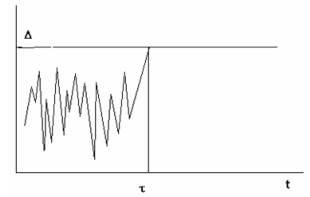
Fig. 2.1 Model de defecțiune instantanee.
Fie ca elementul să acționeze prin supraîncărcarea șocurilor (figura 2.1). Când este mai puțin critică # 8710; nici o defecțiune, nici o deteriorare minoră, deteriorarea caracteristicilor de fiabilitate. Elementul rămâne pentru toți indicatorii drept "nou". Imediat ce supraîncărcarea depășește nivelul critic, elementul eșuează. În cazul în care supraîncărcarea este un proces aleator, cum ar fi zgomotul alb, toate eșantioanele din care sunt independente, istoricul de funcționare în momentul defectării nu este afectat. Adică, un astfel de model de eșec corespunde unei legi exponențiale de fiabilitate.
Neajunsul legii exponențiale este că reflectă un model rar de eșec. Cu toate acestea, se va arăta mai târziu că numai această lege ne permite să construim metode practice de calcul.
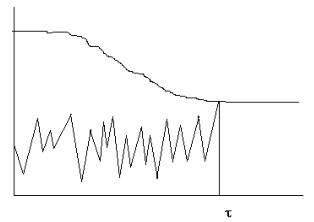
Figura 2.2. O schemă cu un prag variabil.
Luați în considerare o altă schemă de deteriorare instantanee, dar cu un prag care variază în funcție de timp (Figura 2.2). Această schemă diferă de schema prezentată în figura 2.1, deoarece pragul este limita variabilei permise de suprasarcină. La început este mare și supraîncărcarea nu poate ajunge niciodată. Apoi, pragul este redus și la un moment dat t0 este fixat la o anumită valoare constantă, care se obține prin supraîncărcare.
Avem pentru t Pentru t> t0, avem legea exponențială de fiabilitate P (t) = e - # 955; (t-t0) Graficul grafic al probabilității funcționării fără defecțiuni este prezentat în Fig. 2.3. 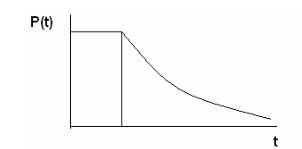
Figura 2.3. Legea cu prag variabil.
Pentru densitatea de probabilitate a eșecului, avem (vezi Figura 2.4):
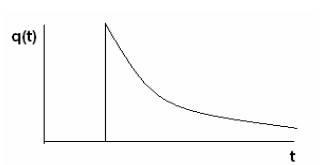
Fig.2.4. Pericol de eșec.
Acest model poate servi ca o aproximare a rezultatelor determinării experimentale a legii de fiabilitate obținută în forma prezentată în Fig. 2.5.
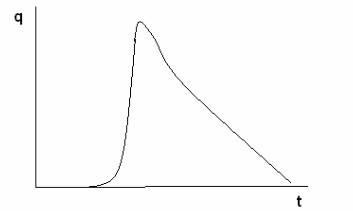
Figura 2.5. Rata eșecului experimental.
1. Care este legea exponențială a fiabilității?
2. În ce raport sunt timpul mediu de funcționare fără probleme și timpul real de funcționare?
3. Descrieți modelul daunelor instantanee.
3. Modelul acumulării daunelor. Gamma - distribuția timpului de funcționare
Modelul de acumulare a daunelor presupune că efectul de perturbări în procesul de exploatare, uzura elementului se acumulează tot timpul, crește. Această acumulare poate să pornească de la condiții inițiale diferite datorită unor mici defecte de producție accidentale, poate crește la rate diferite datorită naturii aleatoare a impactului și așa mai departe.
Să presupunem că există un prag constant, asupra căruia apare defecțiunea (figura 3.1).
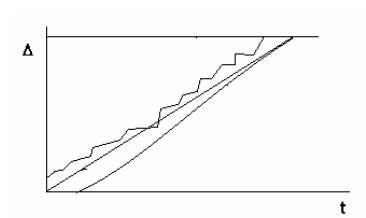
Figura 3.1. Model de acumulare a daunelor.
Luați în considerare următorul model de acumulare a daunelor (figura 3.2).
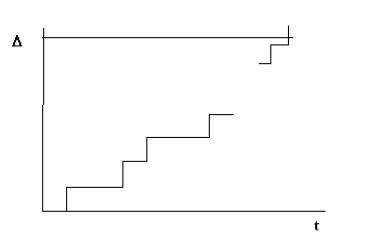
Figura 3.2. Schema acceptată de acumulare a daunelor.
În momente aleatorii independente ale timpului, o creștere a daunelor apare brusc. Toate sarele sunt egale în amplitudine. Considerăm că saltul este egal cu a. De asemenea, presupunem că relația dintre salt și prag este astfel încât eșecul apare după salturi r. Permiteți momentele de sărituri să formeze un flux simplu de evenimente, adică satisface următoarele condiții: evenimentele sunt independente; flux staționar; la un moment dat poate exista doar un singur salt. Se știe că pentru debitul cel mai simplu sau debitul Poisson, probabilitatea de apariție a evenimentelor k exact în timp T este egală cu
aici # 945; este frecvența medie a salturilor.
Eșecul va veni după un număr întreg de sărituri. Atunci funcția P (t) - fiabilitate este probabilitatea ca într-un timp t să existe mai puțin de salturi r
Să găsim densitatea de probabilitate a eșecurilor pentru o astfel de distribuție
Sa obținut o lege de fiabilitate cu doi parametri (# 945; r), care ar putea aproxima caracteristicile experimentale. Dar pentru aceasta este necesar să extindem (3.3) la valori continue ale lui r. În principiu, în (3.3) r poate fi continuu peste tot cu excepția argumentului factorial.
Există o funcție gamma, care pentru valori întregi pozitive ale argumentului coincide cu valoarea factorialului și poate fi adoptată ca extindere a conceptului de valori factoriale la non-integer ale argumentului.
Expresia pentru funcția gamma este
Pentru numere întregi pozitive r, valoarea funcției gamma este
Înlocuirea factorialului cu funcția gamma din (3.3), obținem
Apoi pentru valorile continue ale lui r probabilitatea de defecțiuni este
și funcția de fiabilitate este
Pentru timpul mediu dintre eșecuri, avem
Aici se face substituția x = # 945; # 964; deci d # 964; = dx / # 945;
Pentru funcția gamma, există o relație de recurență, care rezultă din (3.5):
Apoi pentru durata medie de viață de la (3.9) avem:
Observăm că rezultatul obținut este în concordanță cu rezultatele legii exponențiale. Pentru modelul de daune instantaneu, un eveniment este suficient - ajungând la pragul (r = 1), care este independent de istoricul procesului, astfel încât să apară un eșec. Frecvența medie a evenimentelor într-un flux Poisson # 945; în probabilitate este egală cu reciprocitatea timpului mediu dintre eșecurile 1 / T0e pentru legea exponențială de fiabilitate. Prin urmare,
Apoi, pentru legea exponențială din (3.11), obținem rezultatul cunoscut de noi
Pentru dispersia vieții, avem
Aici este luat în considerare faptul că, conform (3.10)
Pericolul de eșec este:
Pericolul de eșec pentru această lege de fiabilitate este calculat într-o manieră complexă. Cu toate acestea, în momentele mici putem lua P (t) ≈ 1; e - # 945; t ≈1, atunci rezultă din (3.6) că dependența de pericolul de expirare are forma (T) ≈ la r -1. ceea ce face posibilă evaluarea comportamentului pericolului de avarie la intervalul inițial. Dependențele exacte sunt prezentate în figura 3.3.
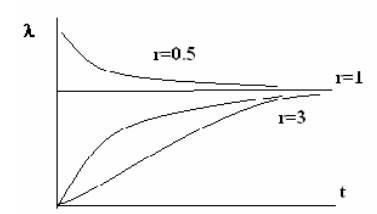
Figura 3.3. Dependența pericolului de defecțiuni asupra parametrului.
Pentru r> 1, avem un model de elemente îmbătrânite (pericolul creșterii eșecului). Pentru r = 1, avem o lege exponențială de fiabilitate. Aceasta corespunde modelului de daune instantanee. Un salt este suficient pentru eșec. Când r<1 имеем убывающую опасность отказа. Частота отказов представлена на рис.3.4. В пределе при r→∞ закон гамма- распределения стремится к нормальному закону надежности.
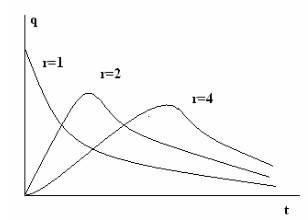
Figura 3.4. Densitatea probabilității defecțiunilor este rata de defecțiune.
1. Descrieți modelul de deteriorare a legii distribuției gama a timpului de funcționare?
2. Care este funcția gamma, de ce este folosită în descrierea legii distribuției gamma?
3. Ce formă are dependența de pericolul eșecului la timp asupra legii distribuției gamma?