Plank hiperboloid x 2 / a 2 + y 2 / b 2 - z 2 / c 2 = 1, a> 0, b> 0, c> 0; Traversat. coordonate osiploskostyami x = 0, y = 0, z = 0 până la hiperbolice y 2 / b 2 - z 2 / c 2 = 1 x 2/2 - z 2 / c 2 = 1 și elipsoidală x 2 / a + y 2 2 / b 2 = 1, respectiv. Secțiunile SSB avioane hiperboloid z = h obținut întotdeauna elipse x 2 / a 2 + y 2 / b 2 = 1 + h 2 / c 2 cu axele și.
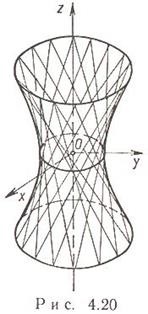
a = b este un hiperboloid cu o singură înclinare de revoluție în jurul axei Oz.
Secțiunile unui hiperboloid dintr-o foaie sunt fie o elipsă, o parabolă, fie o hiperbolă sau o pereche de generatoare drepte (rectilinii).
Printr-un punct arbitrar trec două generatoare rectilinii cu vectori de direcționare și unde:
În special, dacă un punct este ales pe elipsa gâtului, atunci ecuațiile generatoarelor rectilinii vor fi:
Hiperboloid cu două colțuri, ecuația canonică.
doua panze hiperboloid x 2/2 - y 2 / b 2 - z 2 / c 2 = 1, a> 0, b> 0, c> 0; x = h obținută elipsă x 2 / a 2 + z 2 / b 2 = -1 + h2 / c2 cu axele b * rădăcină (h 2 / a 2 -1) și c * root (h 2/2 - 1). Când obținem h = un punct în secțiune (± a, 0,0) - un vârf cu două coli. Secțiile de coordonate pătrat. z = 0 și y = 0 obținem hiperbola x 2/2 - respectiv z 2 / c 2 = 1, - y 2 / b 2 = 1 și x 2 / a 2.
a = b este un hyperboloid cu două colțuri de revoluție în jurul axei Oz.
Secțiuni ale hiperboloidului cu două liste cu avioane: fie o elipsă, fie o hiperbolă sau o parabolă sau un punct.
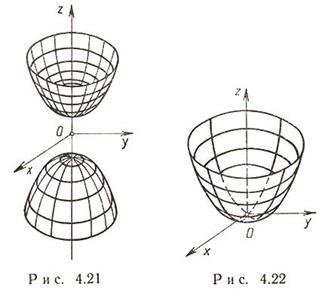
Paraboloid eliptic, ecuația canonică.
eliptic paraboloid x 2 / a 2 + y 2 / b 2 = 2pz a> 0, b> 0;
p = q este paraboloidul revoluției în jurul axei Oz.
Secțiunile paraboloidului eliptic de către planuri sunt fie o elipsă, fie o parabolă, fie un punct.
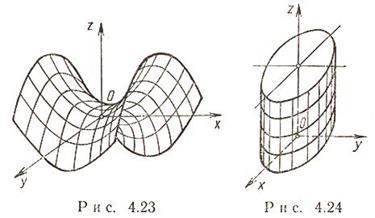
Paraboloidul parabolic, ecuația canonică. Familii de generatoare rectilinie a unui paraboloid hiperbolic.
paraboloidul hiperbolic x 2 / a 2 - y 2 / b 2 = 2pz a> 0, b> 0;
Secțiunile transversale ale unui paraboloid hiperbolic de către avioane - fie o hiperbolă, fie o parabolă sau o pereche de generatoare drepte (rectilinii).
Generatoare de linii drepte
Două generatoare rectilinii trec prin fiecare punct:
O suprafață de rotație este o suprafață formată prin rotirea unei linii plane în jurul unei linii drepte situate în planul acestei linii.
Pentru a deriva ecuația suprafeței de revoluție, este necesar să alegeți un sistem de coordonate. Pentru a face ca ecuația suprafeței de rotație să pară mai simplă, axa de rotație este considerată una dintre axele de coordonate.
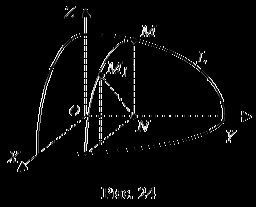
Fie curba L dată în planul de coordonate Oyz prin ecuația F (Y, Z) = 0 (Figura 24). Rotiți curba L în jurul axei Oy. Obținem o suprafață. Fie M (x, y, z) un punct arbitrar al suprafeței rezultate. atunci
. ci pentru că dacă luăm punctul M1 cu un aplicator negativ, atunci
Prin urmare, avem Y = y, iar coordonatele punctului M (x, y, z) satisfac ecuatia
Ecuația (62) este ecuația necesară a suprafeței de rotație.
Astfel. pentru a obține ecuația suprafeței formate prin rotirea liniei L situată în planul Oyz, în jurul axei Oy, este necesar ca ecuația acestei linii să înlocuiască z cu
Reguli similare se vor aplica și ecuațiilor de suprafețe obținute prin rotirea liniilor plane în jurul altor axe de coordonate.
cilindri de ordinul doi: un cilindru eliptic x 2 / a 2 + y 2 / b 2 = 1 a> 0, b> 0; hiperbolic cilindru x 2 / a 2 - y 2 / b 2 = 1 a> 0, b> 0; cilindru parabolic y 2 = 2px; o pereche de planuri intersectate a2x2-b2y2 = 0 a> 0 b> 0 o pereche de planuri paralele sau coincide x-a = 0 a> = 0; linia x 2 + y 2 = 0
conul ordinii a doua x 2 / a 2 - y 2 / b 2 - z 2 / c 2 = 0 a> 0, b> 0, c> 0; Trecerea pl. z = h -> x 2 / a 2 + y 2 / b 2 = 1. În secțiunea transversală prin planurile x = 0, y = 0, avem perechi care intersectează liniile y 2 / b 2 - z 2 / c 2 = 0; x 2 / a 2 - z 2 / c 2 = 0 resp.