Funcțiile de putere, domeniu de definiție.
Băieți, în ultima lecție am învățat cum să lucrăm cu numerele cu un exponent rațional. În această lecție luăm în considerare funcțiile de putere și ne limităm la cazul în care exponentul este rațional.
Vom lua în considerare funcțiile formularului: $ y = x ^> $.
Considerăm mai întâi funcțiile cu exponentul $ \ frac> 1 $.
Să presupunem că avem o funcție specifică $ y = x ^ 2 * 5 $.
Conform definiției pe care am dat-o în ultima lecție: dacă $ x≥0 $, atunci domeniul definiției funcției noastre este raza $ [0; + ∞) $.
Tabel de valori.
Să trecem la cazul în care exponentul este o fracție adecvată (adică atunci când numitorul este mai mic decât numitorul).
Să comparăm cele trei funcții de alimentare: $ y = x ^ 2 $; $ y = x ^ $; $ y = x ^ 3 $.
Numărul 2.5 se situează între 2 și 3, atunci se pare că graficul funcției noastre se va situa între graficele corespunzătoare. Să comparăm valorile funcțiilor pentru diferite x.
1. Dacă $ 0
În prima figură, construim grafice pentru cazul 0 $Proprietățile funcțiilor de alimentare
Proprietățile funcției $ y = x ^> $, $ (m> n) $:
1. $ D (y) = [0; + ∞) $.
2. Nu este nici măcar ciudat.
3. Se mărește cu $ [0; + ∞) $.
4. Nu este limitat mai sus, limitat mai jos.
5. Nu există valoare cea mai mare, cea mai mică valoare este zero.
6. Este continuă.
7. $ E (f) = [0; + ∞) $.
8. Îndoiți-vă.
Graficul grafic al funcției $ y = x ^> $, $ (m> n) $ este similar cu graficul funcției $ y = \ sqrt [n] $. Să schițăm graficul nostru de funcții. 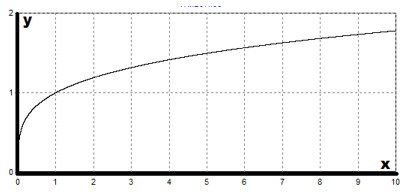
Proprietățile funcției $ y = x ^> $, $ 0 0 $ și r este orice număr rațional, atunci derivatul funcției de putere $ y = x ^ r $ este calculat prin formula: $ y '= r * x ^ $.
Un exemplu. Găsiți cea mai mare și cea mai mică valoare a funcției $ y = x ^> $ pentru intervalul:
a) $ [1; 16] $,
b) $ (2.10) $,
c) pe raza $ [9; + ∞) $.
Soluția.
Exponentul funcției noastre este pozitiv. Apoi, uitându-ne la proprietățile funcției noastre, vedem că ea crește pe întregul domeniu al definiției. Aceasta înseamnă că atinge valoarea sa cea mai mare și cea mai mică la capetele segmentelor date (dacă este definită la aceste puncte).
a) $ y_ = 1 ^> = 1 $; $ y_ = 16 ^> = (\ sqrt) ^ 5 = 4 ^ 5 = 1024 $.
b) Nu există valoare maximă și minimă a funcției pe acest interval, deoarece avem un interval deschis și punctele 0 și 4 nu aparțin acestui interval.
c) Cea mai mare valoare nu este.
$ y_ = 9 ^> = \ sqrt = (\ sqrt) ^ 5 = 3 ^ 5 = 243 $.
Un exemplu. Găsiți cea mai mare și cea mai mică valoare a funcției: $ y = \ fracx ^> - \ fracx ^ 4 $ pe intervalul $ [1; 9] $.
Soluția.
Băieți, vă amintiți cum am găsit cea mai mare și cea mai mică valoare a unei funcții pe un segment din clasa 10?
Corect, am folosit un derivat. Să rezolvăm exemplul nostru și să repetăm algoritmul pentru găsirea celei mai mici și mai mari valori.
1. Să găsim derivatul unei funcții date:
$ y '= \ frac * \ fracx ^> - x ^ 3 = 8x ^> - x ^ 3 = 8 \ sqrt-x ^ 3 $.
2. Derivatul există pe întregul domeniu al definirii funcției inițiale, atunci nu există puncte critice. Să găsim punctele staționare:
$ y '= 8 \ sqrt-x ^ 3 = 0 $.
$ 8 * \ sqrt = x ^ 3 $.
$ 64x ^ 3 = x ^ 6 $.
$ x ^ 6-64x ^ 3 = 0 $.
$ x ^ 3 (x ^ 3-64) = 0 $.
$ x_1 = 0 $ și $ x_2 = \ sqrt [3] = 4 $.
Segmentul dat conține o singură soluție $ x_2 = 4 $.
Construim un tabel de valori al funcției noastre la capetele segmentului și la punctul extrem:
Răspunsul este: $ y _ = - $ 862.65 $ pentru $ x = 9 $; $ y_ = 38,4 $ pentru $ x = 4 $.
Un exemplu. Rezolvați ecuația: $ x ^> = 24-x $.
Soluția. Graficul grafic al funcției $ y = x ^> $ crește, iar graficul funcției $ y = 24-x $ scade. Băieți, știm că dacă o funcție crește și cealaltă scade, atunci se intersectează doar la un punct, adică avem doar o singură soluție.
Notă:
$ 8 ^ = = sqrt [3] = (\ sqrt [3]) ^ 4 = 2 ^ 4 = 16 $.
$ 24-8 = 16 $.
Asta este, pentru $ x = 8 $ avem egalitatea corectă $ 16 = 16 $, aceasta este soluția ecuației noastre.
Răspunsul este $ x = 8 $.
Un exemplu.
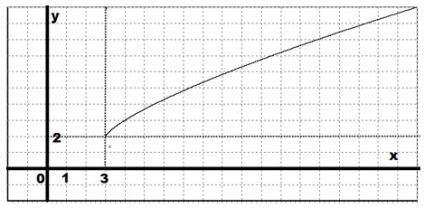
Construiți un grafic al funcției: $ y = (x-3) ^ \ frac + 2 $.
Soluția.
Graficul grafic al funcției noastre este obținut din graficul funcției $ y = x ^> $, trecând 3 unități spre dreapta și 2 unități în sus.
Un exemplu. Scrieți ecuația tangentei la linia $ y = x ^> $ în punctul $ x = 1 $.
Soluția. Ecuația tangentei este determinată de formula cunoscută de noi:
$ a = f (a) + f '(a) (x-a) $.
În cazul nostru, $ a = 1 $.
$ f (a) = f (1) = 1 ^ 1 = 1 $.
Să găsim derivatul:
$ y '= - \ fracx ^> $.
Calculăm:
$ f '(a) = - \ frac * 1 ^> = - \ frac $.
Să găsim ecuația tangentei:
$ y = 1 - \ frac (x-1) = - \ fracx + 1 \ frac $.
Răspunsul este: $ y = - \ fracx + 1 \ frac $.
Sarcini pentru soluții independente
1. Gasiti cea mai mare si cea mai mica valoare a functiei: $ y = x ^ \ frac $ pe segment:
a) $ [1; 8] $.
b) $ (4.50) $.
c) pe raza $ [27; + ∞) $.
2. Gasiti cea mai mare si cea mai mica valoare a functiei $ y = \ fracx ^> - x $ pe intervalul $ [1; 27] $.
3. Rezolvați ecuația: $ x ^> = 18-x $.
4. Construiește un grafic al funcției: $ y = (x + 1) ^> - 1 $.
5. Scrieți ecuația tangentei la linia $ y = x ^> $ în punctul $ x = 1 $.