Generator de numere pseudo-aleatoare bazat pe algoritmul BBS
La fiecare etapă n-a a funcționării generatorului se calculează xn + 1 = xn 2 mod M. Rezultatul etapei n este un bit (de obicei mai mic) al numărului xn + 1. Uneori bitul de paritate este folosit ca rezultat, adică numărul de unități în reprezentarea binară a elementului. Dacă numărul de unități din intrarea numerică este egal, bitul de paritate este setat la 0. Impar - bitul de paritate este setat la 1.
De exemplu. lăsați p = 11, q = 19 (suntem convinși că 11 mod 4 = 3, 19 mod 4 = 3). Apoi M = p * q = 11 * 19 = 209. Alegeți x. este relativ prime la M. Fie x = 3. Să calculăm numărul de pornire al generatorului x0:
Calculăm primele zece numere xi de algoritmul BBS. Ca biți aleatorii, luăm cel mai puțin semnificativ bit în reprezentarea binară a numărului xi:
Cea mai interesantă proprietate a acestei metode este aceea că pentru a obține numărul n de la o secvență nu este necesar să se calculeze toate numerele n anterioare xi. Se pare că xn poate fi obținut imediat din formula
De exemplu, calculați x10 de la x0 simultan:
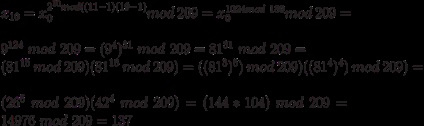
Drept rezultat, într-adevăr a obținut aceeași valoare. ca în cazul calculului secvențial, 137. Computările par a fi destul de complexe, însă, de fapt, ele sunt ușor de formalizat sub forma unei mici proceduri sau de programe și se utilizează dacă este necesar.
Abilitatea de a obține "direct" xn vă permite să utilizați algoritmul BBS pentru criptarea streaming, de exemplu, pentru accesarea de fișiere aleatoriu sau fragmente de fișiere cu înregistrări de bază de date.
Siguranța algoritmului BBS se bazează pe complexitatea descompunerii unui număr mare M în multiplicatori. Se afirmă că dacă M este suficient de mare, acesta nu poate fi ținut secret; până când M este factorizat, nimeni nu va putea să prezică rezultatul generatorului PSC. Acest lucru se datorează faptului că problema extinderii numărului de forme n = pq (p și q - numere prime) în multiplicatori este foarte dificilă computațional dacă știm doar n. și p și q sunt numere mari compuse din mai multe zeci sau sute de biți (aceasta este așa numita problemă de factorizare).
În plus, puteți dovedi că atacatorul. cunoscând o anumită secvență generată de generatorul BBS. Nu va putea determina nici biții anteriori înaintea lui, nici următorii. Generatorul BBS este imprevizibil în direcția stângă și în direcția cea bună. Această proprietate este foarte utilă în scopul criptografiei și este de asemenea legată de singularitățile factorizării numărului M.
Cel mai important dezavantaj al algoritmului este acela că nu este suficient de rapid ca acesta să nu permită utilizarea acestuia în multe domenii, de exemplu, în calcule în timp real și, din păcate, de asemenea, cu criptare în flux.
Dar acest algoritm produce o succesiune foarte bună de numere pseudo-aleatoare cu o perioadă lungă (cu o alegere adecvată a parametrilor inițiali), ceea ce permite utilizarea acestuia în scopuri criptografice atunci când se generează chei pentru criptare.
Termeni-cheie
Ciflul de flux este un cifru de flux.
Generatorul de numere generatoare de pseudo-aleatoare (GPRS) este un algoritm sau un dispozitiv care creează o secvență de biți care arată ca una aleatorie.
Un generator de numere pseudorandomice congruiale liniar este unul dintre cele mai simple GPRS care utilizează formula ki = (a * ki-1 + b) mod c pentru a calcula următorul număr ki. unde a, b, c sunt câteva constante. a ki-1 este numărul anterior pseudo-aleator.
Metoda retardată de Fibonacci este una dintre metodele de generare a numerelor pseudo-aleatoare. Poate fi folosit în criptografie.
Un cifru de flux este un cifru. care efectuează criptarea mesajului de intrare un bit (sau octet) per operație. Un algoritm de criptare streaming elimină necesitatea de a împărți un mesaj într-un număr întreg de blocuri. Cipurile de flux sunt utilizate pentru criptarea datelor în timp real.
Rezultatele rezumate
Un cifru de flux este un cifru. care efectuează criptarea mesajului de intrare un bit (sau octet) per operație. Un algoritm de criptare streaming elimină necesitatea de a împărți un mesaj într-un număr întreg de blocuri. Astfel, dacă se transmite un flux de caractere, fiecare caracter poate fi criptat și transmis imediat. Cipurile de flux sunt utilizate pentru criptarea datelor în timp real.
Ca generatoare de chei în cipuri de fluxuri, pot fi utilizate generatoare de numere pseudo-aleatoare (GPRS). Scopul utilizării GPRS este obținerea unui cuvânt cheie "infinit", care are o lungime relativ mică a cheii în sine. Pentru utilizarea în scopuri criptografice, generatorul de numere pseudo-aleatoare trebuie să aibă anumite proprietăți, de exemplu, perioada de secvență generată de generator trebuie să fie foarte mare.
Cele mai simple generatoare de numere pseudo-aleatoare sunt: un generator liniar congruential. generator prin metoda Fibonacci cu întârzieri, generator bazat pe algoritmul Blum-Blum-Shuba (BBS).
Setați pentru practică
Întrebări pentru auto-examinare
- Cum diferă fluxul de cifru de cifrul de bloc?
- Cum este organizată criptarea unui flux de date cu lungime variabilă?
- Ce numere sunt numite "pseudorandom"?
- Ce proprietăți trebuie să aibă un generator de numere pseudo-aleatoare pentru utilizare în scopuri criptografice?
- Ce fel de generatoare de numere pseudo-aleatoare poti numi?
- Listați principalele caracteristici, avantaje și dezavantaje ale fiecărui generator de numere pseudo-aleatoare considerat în această prelegere.
Exerciții pentru auto-examinare
- Determinați secvența primelor zece numere și perioada generatorului congruențial liniar PSC pentru diferiți parametri a, b și c (k0 este luat ca 0):
- a = 5, b = 7 și c = 17;
- a = 6, b = 3 și c = 23.
- a = 3, b = 1, k0 = 0,6; k1 = 0,3; k2 = 0,5;
- a = 4, b = 2, k0 = 0,9; k1 = 0,3; k2 = 0,5; k3 = 0,9.