Printr-un acord special cu comisia editorială și cu comitetul editorial al revistei Quantum
În rezolvarea problemelor mecanice, utilizarea conceptului de centru al masei unui sistem de puncte materiale poate fi de neprețuit. Unele sarcini nu pot fi rezolvate fără a recurge la acest concept, soluția celorlalți cu ajutorul lui poate deveni mult mai ușoară și mai vizibilă.
Înainte de a discuta probleme specifice, amintim principalele proprietăți ale centrului de masă și le ilustrăm cu exemple.
Centrul de masă (centrul de masă) al unui sistem de puncte materiale este un punct care caracterizează distribuția maselor într-un sistem a cărui coordonate sunt date de formule
Aici mi sunt masele punctelor materiale care formează sistemul, xi. yi. zi sunt coordonatele acestor puncte. Cititorii familiarizați cu conceptul unui vector de rază vor prefera o notație vectorială:
Exemplul 1. Să găsim poziția centrului de masă, cel mai simplu sistem alcătuit din două puncte ale căror mase m1 și m2 și distanța dintre acestea l (Fig.
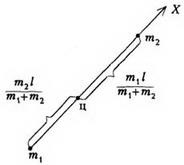
Prin direcționarea axei X de la primul punct la cel de-al doilea, constatăm că distanța de la primul punct la centrul de masă (adică coordonatul centrului de masă) este egală cu distanța de la centrul de masă la al doilea punct este egală cu. raportul de distanțe înapoi la raportul de masă. Prin urmare, în acest caz, poziția centrului de masă coincide cu centrul de greutate.
1) Poziția centrului de masă nu se modifică dacă o parte a sistemului este înlocuită de un singur punct cu o masă egală cu masa acestui subsistem și situată la centrul său de masă.
Exemplul 2. Luați în considerare un triunghi plat omogen și găsiți poziția centrului său de masă. Împărțiți triunghiul în benzi subțiri paralele cu una din laturi și înlocuiți fiecare bandă cu un punct situat în mijlocul acesteia. Deoarece toate aceste puncte se află pe mediana triunghiului, centrul de masă trebuie să se afle și pe mediană. Repetând argumentele pentru fiecare parte, constatăm că centrul de masă se află la intersecția medianilor.
2) Viteza centrului de masă poate fi găsită prin luarea derivării timpului de ambele părți ale (1):
unde este impulsul sistemului, m este masa totală a sistemului. Se poate observa că viteza centrului de masă al unui sistem închis este constantă. Prin urmare, dacă asociem un cadru de referință în mișcare cu centrul de masă, atunci acesta va fi inerțial.
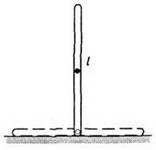
Exemplul 3. Să punem un tija uniformă de lungime l pe verticală pe un plan neted (fig.2) și să lăsăm drumul. În procesul de cădere, atât componenta orizontală a impulsului său, cât și componenta orizontală a vitezei centrului de masă vor rămâne egale cu zero. Prin urmare, în momentul căderii, centrul tijei va fi în locul în care tija a fost inițial, iar capetele tijei se vor mișca orizontal.
3) Accelerarea centrului de masă este egală cu derivatul vitezei sale în raport cu timpul:
unde în partea dreaptă a ecuației există doar forțe externe, deoarece toate forțele interne sunt contractate conform celei de-a treia legi a lui Newton. Observăm că centrul de masă se mișcă ca un punct imaginar care se mișcă cu o masă egală cu masa sistemului sub acțiunea forței externe care rezultă. Probabil, aceasta este cea mai fizică proprietate a centrului de masă.
Exemplul 4: Dacă arunci un băț, aducându-l în același timp în rotație, centrul de masă al bățul (mijlocul acesteia) se va deplasa cu o accelerație constantă de-a lungul unei parabole (Fig. 3).
4) Lăsați sistemul de puncte să fie într-un câmp gravitațional omogen. Apoi, momentul total de gravitație în raport cu orice axă care trece prin centrul de masă este zero. Aceasta înseamnă că rezultatul forțelor de gravitație trece prin centrul de masă, adică centrul de masă este, de asemenea, centrul de greutate.
5) Energia potențială a unui sistem de puncte într-un câmp gravitațional omogen este calculată din formula
unde h, este înălțimea centrului de masă al sistemului.
Exemplul 5. Când se săpare un puț într-o lire omogenă de adâncime h și se răspândește solul de-a lungul suprafeței, energia sa potențială crește cu, unde m este masa solului extras.
6) Și încă o proprietate utilă a centrului de masă. Energia cinetică a sistemului de puncte poate fi reprezentat ca o sumă a doi termeni: energia cinetică totală a mișcării de translație a sistemului egal și cinetică Eotn energia mișcării în raport cu cadrul asociat cu centrul de masă:
Exemplul 6. Energia cinetică a unui rulou de rulare fără alunecare pe o suprafață orizontală cu viteza υ este
deoarece mișcarea relativă în acest caz este o rotație pură, pentru care viteza liniară a punctelor din cerc este egală cu υ (viteza totală a punctului de fund trebuie să fie zero).
Acum vom începe să analizăm sarcinile pentru utilizarea centrului de masă.
Problema 1. O tijă omogenă se află pe o suprafață orizontală netedă. Două forțe de aceeași mărime, dar opuse în direcția forțelor orizontale sunt aplicate pe tija: o forță este aplicată la mijlocul tijei, cealaltă la capătul său (Figura 4). În ce punct începe să se transforme tija?
La prima vedere poate părea că axa de rotație este un punct situat în mijloc între punctele de aplicare a forțelor. Cu toate acestea, ecuația (3) arată că, deoarece suma forțelor exterioare este zero, accelerația centrului de masă este zero. Prin urmare, centrul tijei va rămâne în repaus, adică servesc ca axă de rotație.
Problema 2. O bară omogenă subțire cu lungimea l și masa m este condusă de-a lungul unei suprafețe orizontale netede, astfel încât aceasta se mișcă transversal și simultan se rotește cu viteza unghiulară ω. Găsiți tensiunea barei în funcție de distanța x până la centrul acesteia.
Să trecem la cadrul de referință inerțial, legat de centrul tijei. Să considerăm mișcarea unei bucăți de tija închisă între punctul considerat al tijei (situat la o distanță x față de centru) și capătul său (figura 5).
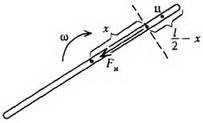
Singura forță externă pentru această piesă este forța de tensionare dorită Fn. masa este egală, iar centrul ei de masă se deplasează de-a lungul circumferinței printr-o rază cu accelerație. Scriind ecuația de mișcare a centrului de masă al piesei selectate, obținem
Problema 3. O stea dublă constă din stele cu două componente cu mase m1 și m2. distanța dintre care nu se schimbă și rămâne egală cu L. Găsiți perioada de rotație a stelei duble.
Să considerăm mișcarea stelelor componente într-un cadru de referință inerțial, legat de centrul de masă al unei stele binare. În acest cadru de referință, stelele se mișcă cu aceeași viteză unghiulară de-a lungul cercurilor de diferite raze (figura 6).
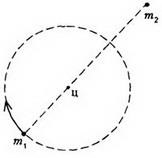
Raza de rotație a unei stele cu masa m1 este egală (a se vedea exemplul 1), iar accelerația centripetală este creată de forța de atracție către o altă stea:
Vedem că perioada de rotație a unei stele duble este egală cu
și este determinată de masa totală a stelei binare, indiferent de modul în care este distribuită între stelele componente.
Problema 4. Masele cu două puncte m și 2 m sunt conectate printr-un fir fără greutate de lungime l și se deplasează de-a lungul unui plan orizontal neted. La un moment dat, viteza de masă 2m este zero, iar viteza de masă m este egală cu υ și este direcționată perpendicular pe filament (figura 7). Găsiți tensiunea firului și perioada de rotație a sistemului.
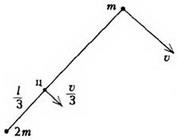
Centrul de masă al sistemului se află la o distanță de masa de 2 metri și se mișcă la o viteză. Într-un cadru de referință conectat la centrul de masă, un punct de masă de 2 m se deplasează de-a lungul circumferinței cu o rază cu viteză. Prin urmare, perioada de rotație este egală cu (verificați dacă același răspuns este obținut dacă luăm în considerare un punct de masă m). Gasim tensiunea filamentului din ecuatia de miscare a oricareia din cele doua puncte:
Problema 5. Pe un plan orizontal neted există două bare identice de masă m fiecare, conectate printr-un arc de lumină cu rigiditate k (figura 8). Prima bară are o viteză υ0 în direcția de la a doua bară. Descrieți mișcarea sistemului. După ce timp devine prima deformare a primăverii valoarea maximă?
Centrul de masă al sistemului se va deplasa cu o viteză constantă. Centrul cadrului masei de referință a vitezei inițiale egală cu fiecare bară, iar arcul jumătate de rigiditate, care se conecteaza la centrul fix al masei este 2k (rigiditate arc este invers proporțională cu lungimea sa). Perioada acestor oscilații este
și amplitudinea oscilațiilor fiecărui bare, care poate fi găsită din legea conservării energiei, este
Pentru prima dată, deformarea va deveni maximă după un sfert din perioada respectivă, adică prin timp.
Problema 6. O minge de masa m zboara cu viteza υ pe o minge de odihna cu masa de 2m. Găsiți vitezele ambelor bile după un impact central elastic.
În sistemul de referință asociat cu centrul de masă, impulsul total al celor două bile egale cu zero, atât înainte cât și după sus coliziuni. Este ușor să ghicească răspunsul la final satisface viteză atât starea și legea de conservare a energiei: viteza va rămâne aceeași ca înainte de impact, în magnitudine, dar se va schimba direcția spre opusul. Viteza centrului de masă al sistemului este. Centrul sistemului de masă, prima minge se deplasează cu o viteză, iar al doilea mingea se deplasează spre prima viteza cu. După impact, bilele vor zbura cu aceleași viteze. Rămâne să reveniți la cadrul original de referință. Aplicarea legii adăugarea de viteze, constatăm că viteza finală a mingea este egală cu masa m și este îndreptată înapoi, iar viteza de minge, înainte de 2m masă de repaus și este îndreptată înainte.
Observăm că în sistemul centrului de masă este evident că atunci când se aplică impactul, viteza relativă a bilelor nu se modifică în magnitudine, dar variază în direcție. Și deoarece diferența de viteză nu se schimbă în trecerea la un alt cadru de referință inerțial, putem presupune că am derivat această relație importantă pentru cadrul inițial de referință:
unde litera υ este folosită pentru a desemna vitezele inițiale și u - pentru vitezele finale. Această ecuație poate fi rezolvată împreună cu legea conservării impulsului în loc de legea conservării energiei (unde vitezele intră în a doua putere).
Problema 7. Se știe că pentru un impact elastic noncentral al două bile identice, dintre care unul a fost în repaus înainte de impact, unghiul de expansiune este de 90 °. Dovediți această declarație.
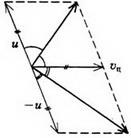
În sistemul centrului de masă, impactul noncentral poate fi descris după cum urmează. Înainte de a lovi bilele vin împreună cu același impuls, după impactul pe care zbura cu aceeași magnitudine dar Impulsul opuse și de expansiune directă este rotită cu un anumit unghi în raport cu abordarea directă. Pentru a vă întoarce la cadrul inițial de referință, este necesar să adăugați fiecare viteză finită (vectorial!) Cu viteza centrului de masă. În cazul centrului bile identic al vitezei de masa este locul unde υ - viteză de minge de intrare și centrul cadrului masei de bile de referință converg și împrăștie cu viteze egale. Faptul că, după fiecare adăugare de viteza finală cu centrul vitezei de masă obținută prin vectori perpendiculare între ele, se poate vedea din Figura 9. poate verifica pur și simplu că produsul scalar al vectorilor și dispare datorită faptului că modulele vectorilor sunt egale între ele.
1. O tijă de masă m și lungimea l este articulată la unul dintre capete. Tija a fost deviată la un unghi din poziția verticală și eliberată. În momentul trecerii poziției verticale, viteza punctului inferior este egală cu υ. Găsiți tensiunea la mijlocul tijei în acest moment.
2. O tijă de masă m și lungimea l este rotită într-un plan orizontal cu o viteză unghiulară ω în jurul unuia dintre capetele sale. Identificați dependența tensiunii tijei de distanța x față de axa de rotație, dacă la celălalt capăt este fixată o greutate mică cu masa M.
3. Găsiți perioada de oscilație pentru sistemul descris în Problema 5 a hârtiei, dar pentru barele de mase diferite m1 și m2.
4. Derulați formulele generale cunoscute pentru impactul central elastic al celor două bile, folosind tranziția către centrul sistemului de referință al masei.
5. O minge de masă m1 lovește o minge de odihnă de mărime mai mică m2. Găsiți unghiul maxim posibil de deformare a balonului incident în cazul unui impact elastic necentral.