Care este algebra logicii?
Algebra logică (algebra booleană) este o ramură a matematicii care a apărut în secolul al XIX-lea datorită eforturilor matematicienului englez J. Boole. La început, algebra booleană nu avea nici o semnificație practică. Cu toate acestea, deja în secolul al XX-lea, dispozițiile sale au fost aplicate în descrierea funcționării și dezvoltării diferitelor circuite electronice. Legile și aparatele de algebră a logicii au început să fie utilizate în proiectarea diferitelor părți ale computerelor (memorie, procesor). Deși aceasta nu este singura sferă de aplicare a acestei științe.
Care este algebra logicii? În primul rând, ea studiază metodele de stabilire a adevărului sau falsității unor declarații logice complexe folosind metode algebrice. În al doilea rând, algebra booleană face acest lucru astfel încât o declarație logică complexă este descrisă de o funcție al cărei rezultat poate fi adevărat sau fals (1 sau 0). În acest caz, argumentele funcției (instrucțiuni simple) pot avea și două valori: 0 sau 1.
Ce este o simplă declarație logică. Acestea sunt fraze ca "două mai mult de unu", "5.8 este un număr întreg". În primul caz, avem adevărul și în cea de-a doua minciună. Algebra logică nu se referă la esența acestor afirmații. Dacă cineva decide că "Pământul este pătrat" este adevărat, atunci algebra logicii o va lua ca un fapt. Ideea este că algebra booleană este implicată în calculul rezultatului unor declarații logice complexe, bazate pe valorile cunoscute anterior ale simplelor declarații.
Operații logice. Disjuncție, conjuncție și negare
Deci, cum comunică simple declarații logice, formând cele complexe? Într-o limbă naturală, folosim diferite sindicate și alte părți ale discursului. De exemplu, "și", "sau", "fie", "nu", "dacă", "care", "atunci". " Un exemplu de declarații complexe: "el are cunoștințe și abilități", "va veni marți sau miercuri", "voi juca atunci. când îmi fac temele "," 5 nu este 6 ". Cum decidem dacă ne-au spus adevărul sau nu? Cumva logic, chiar și undeva în mod inconștient, bazat pe experiența vieții anterioare, înțelegem că adevărul în cadrul alianței "și" vine în cazul veridicității celor două simple propoziții. Merită să devină o minciună și toată declarația complicată va fi înșelătoare. Dar, cu conexiunea "fie", o singură declarație simplă ar trebui să fie adevărată, iar apoi întreaga expresie va deveni adevărată.
Algebra booleană a schimbat această experiență de viață în aparatul de matematică, a formalizat-o, a introdus reguli rigide pentru obținerea unui rezultat neechivoc. Sindicatele au ajuns să fie numite operatori logici aici.
Algebra logică oferă multe operații logice. Cu toate acestea, trei dintre ele merită o atenție deosebită. cu ajutorul acestora puteți descrie toate celelalte și, prin urmare, utilizați mai puține dispozitive diferite atunci când proiectați circuite. Astfel de operații sunt conjuncția (AND), disjuncția (OR) și negarea (NOT). Adesea se indică conjuncția . disjuncție - ||. și negarea este o bară peste o variabilă care denotă o declarație.
Cu conjuncție, adevărul unei expresii complexe apare numai în cazul adevărului tuturor expresiilor simple, din care constă complexul. În toate celelalte cazuri, expresia complexă va fi falsă.
În disjuncție, adevărul unei expresii complexe apare atunci când există cel puțin o expresie simplă sau două care intră imediat în ea. Se întâmplă că o expresie complexă constă din mai mult de două simple. În acest caz, este suficient ca unul simplu să fie adevărat și atunci întreaga afirmație este adevărată.
Negarea este o operație unară, deoarece este efectuată cu privire la o expresie simplă sau la rezultatul unui rezultat complex. Ca urmare a negării, se obține o nouă declarație, care este opusul celei originale.
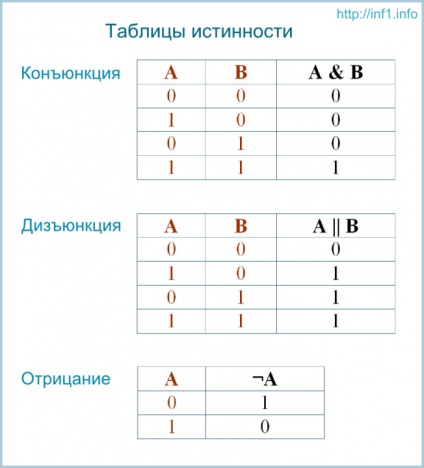
Tabele de adevăr
Operațiile logice sunt descrise convenabil prin așa-numitele tabele de adevăr. în care se reflectă rezultatele calculelor de declarații complexe pentru diferite valori ale cuvintelor simple originale. Declarațiile simple sunt indicate prin variabile (de exemplu, A și B).
Baza logică a calculatorului
În computer se folosesc diverse dispozitive, ale căror lucrări sunt descrise perfect prin algebra logică. Astfel de dispozitive includ grupuri de comutatoare, declanșatoare, totalizatoare.
În plus, legătura dintre algebra booleană și calculatoare se găsește în sistemul numeric utilizat în computer. După cum știți, este binar. Prin urmare, în dispozitivele calculatorului este posibilă stocarea și conversia atât a numerelor, cât și a valorilor variabilelor logice.
Circuite de comutare
În computer se utilizează circuite electrice, constând dintr-o multitudine de întrerupătoare. Comutatorul poate fi în două stări: închis și deschis. În primul caz - trece curent, în al doilea - nr. Descrieți funcționarea unor astfel de scheme este foarte convenabilă cu ajutorul algebrei logice. În funcție de poziția comutatoarelor, puteți primi sau nu primi semnale la ieșiri.
Porți, declanșatoare și aditivi
O supapă este un element logic care ia o valoare binară și eliberează altele în funcție de implementarea sa. De exemplu, există porți care implementează înmulțirea logică (conjuncție), adăugarea (disjuncția) și negarea.
Declanșatoarele și dispozitivele de declanșare sunt dispozitive relativ complexe, constând din elemente simple - porți.
Triggerul poate stoca o cifră binară, datorită faptului că poate fi în două stări stabile. Practic, declanșatoarele sunt utilizate în registrele procesoarelor.
Sumatorii sunt folosiți pe scară largă în unitățile logice aritmetice (ALU) ale procesorului și efectuează sumarea cifrelor binare.
Imaginile utilizate în articol