13. Algoritmi de căutare, selecție și sortare.
Algoritmul de căutare secvențială (APT) scanează secvențial un element din listă, începând cu primul, până când găsește elementul țintă. Se presupune că lista nu este sortată.
Cel mai rău caz: elementul țintă este ultimul element din listă sau nu este pe lista deloc.
Un caz mediu: căutarea se încheie întotdeauna cu succes sau, uneori, valoarea țintă nu este listată.
Algoritmul de căutare binar (ADD):
Căutarea binară se efectuează pe lista sortată. Ideea este ca lista sa fie impartita pe jumatate, media el-t este luata si comparata cu el-tom-ul tinta. Când se face o comparație, este posibil unul din cele trei rezultate: valorile sunt egale, valoarea țintă este mai mică decât elementul listă sau valoarea țintă este mai mare decât elementul din listă. În primul și cel mai bun, cazul este finalizat. În celelalte două cazuri, putem renunța la jumătate din listă. Atunci când valoarea țintă este mai mică decât elementul mediu, știm că dacă se află în listă, se află în fața acestui element intermediar. Când este mai mult decât elementul mediu, știm că dacă este în listă, este după acest element intermediar. Acest lucru este suficient pentru a putea renunța la o jumătate din listă printr-o singură comparație. Dacă se repetă această procedură, putem renunța la jumătate din partea rămasă din listă.
În cel mai rău caz, numărul de treceri este k = log2 (N + 1).
Cazul mediu A (N) ≈ log2 (N + 1) -1
Uneori avem nevoie de un e-mail din lista, care are unele mesaje speciale, dar nu are nici un sens specific. De exemplu, în lista angajaților găsiți vârsta medie sau găsiți 5 salariați cu cel mai mic salariu. Într-un caz mai general, s-ar putea să fim interesați să scriem cu cea mai mare valoare a câmpului. O modalitate de a găsi o astfel de înregistrare este să sortați lista în ordine descrescătoare; atunci înregistrarea cu cea mai mare valoare K va fi pe locul K. Acest lucru va necesita mult mai multă energie decât este necesar: valori mai puțin decât ceea ce căutăm, de fapt, nu ne interesează. Următoarea abordare poate fi utilă: găsim cea mai mare valoare în listă și o plasăm la sfârșitul listei. Apoi găsim cea mai mare valoare în restul listei, cu excepția celui deja găsit. Ca rezultat, obținem cea de-a doua valoare cea mai mare a listei, care poate fi plasată pe cea de-a doua de la sfârșitul listei. Dacă repetăm această procedură K ori, găsim cea mai mare valoare K.
La fiecare pas al algoritmului, selectăm unul din elementele de date de intrare și îl inserăm în poziția dorită în lista deja sortată, până când setul de date de intrare este epuizat. Metoda de selectare a următorului element al șirului sursă este arbitrară; aproape orice algoritm de alegere poate fi utilizat. De obicei (și pentru a obține un algoritm de sortare stabil), elementele sunt inserate în ordinea apariției lor în matricea de intrare. Algoritmul de mai jos folosește această strategie de selecție particulară.
Intrare: matricea A, constând din elemente A [1], A [2]. A [n]
în timp ce j> 0 și A [j]>:
Timpul de execuție al algoritmului depinde de datele de intrare: cu cât este mai mare setarea setului, cu atât este mai mare sortarea. De asemenea, ordonarea inițială a matricei afectează timpul de execuție. Deci, cel mai bun caz este matricea sortată, iar cea mai rea este matricea sortată în ordinea inversă față de cea dorită. Complexitatea temporală a algoritmului cu cea mai slabă variantă a datelor de intrare este θ (n²).
Algoritmul constă în treceri repetate prin matricea sortată. Pentru fiecare trece elementele comparate succesiv reciproc, iar în cazul în care ordinea în pereche nu este corectă, elementele sunt schimbate. Pasajul de-a lungul matricei se repetă până când următoarea trecere arată că schimburile nu mai sunt necesare, ceea ce înseamnă că matricea este sortată. Când algoritmul trece, un element care nu este în locul său, "plutește" în poziția dorită ca un balon în apă, de unde și numele algoritmului.
Când sortați Shell, mai întâi comparați și sortați valorile care sunt distanțate unul de celălalt la o anumită distanță d. După aceasta, procedura este repetată pentru unele valori mai mici ale lui d, iar sortarea lui Schell este completă prin comanda elementelor la d = 1 (adică sortarea obișnuită a inserțiilor). Eficacitatea sortimentării Shell în anumite cazuri este asigurată de faptul că elementele "repede" intră în vigoare.
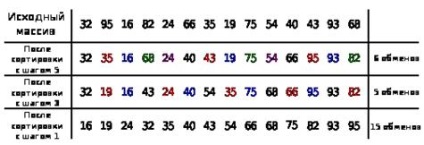
Un exemplu. Având în vedere o listă A = (32,95,16,82,24,66,35,19,75,54,40,43,93,68) și sortarea sa realizat de Shell, și ca și valorile d selectat 5,3 , 1.
In sublists primul pas sortate A, format din toate elementele A, care diferă de 5 poziții, adică sublists A5,1 = (32,66,40), A5,2 = (95,35,43), A5,3 = ( 16,19,93), A5,4 = (82,75,68), A5,5 = (24,54).
În lista primită, în al doilea pas, sub-elementele din elementele care sunt separate prin 3 elemente sunt sortate din nou.
Procesul se termină cu sortarea obișnuită a inserțiilor din lista rezultată.
Lista generală este împărțită în stive în funcție de rangul cheii. La fiecare trecere, permutările sunt efectuate în conformitate cu valoarea unei părți separate a cheii. După fiecare trecere, stivele sunt stivuite și împărțite într-o altă categorie cheie.
Un algoritm de sortare recursivă. După selectarea unui element din listă, sortarea rapidă o împarte în două părți. Într-o parte, elementele sunt mai selecționate, în cealaltă - mai puțin.
Un algoritm de sortare care organizează liste (sau alte structuri de date a căror acces la elemente poate fi obținut numai secvențial, de exemplu - fire) într-o anumită ordine.
- Poziția de sortare este împărțită în două părți de aproximativ aceeași dimensiune;
- Fiecare dintre piesele rezultate este sortată separat, de exemplu - prin același algoritm;
- Două magnitudine ordonate sunt îmbinate într-una.
Despărțirea recursivă a problemei în cele mai mici are loc până când dimensiunea matricei ajunge la unitate (orice matrice de lungime 1 poate fi considerată ordonată).