Semigrupul idempotent

un semigrup idempotent, este o grupare semigrup, fiecare element al căruia este idempotent. N. ca un ciorchine (acest lucru este în concordanță cu conceptul de SEMIGRUPURI fascicule: .. Și există o grămadă de semigrupuri cu un singur element de n). Se numește o algebră liniară comutativă. semi-structură sau semilattică; acest termen este în concordanță cu utilizarea sa în teoria seturilor parțial ordonate :. I. comutativ dacă n Srassmotret conform ordinii parțiale naturale, ab este cel mai mare inferior legat Fiecare element este semilattice doua elemente semilattices subdirect produs. Semigrupa Sn. singular dacă S satisface una dintre identitățile xy = x, xy = y, în primul caz Sn. levosingulyarnoy sau semigrup de zerouri la stânga în al doilea - pravosingulyarnoy sau semigrupul de zerouri din dreapta. Se spune că este un semigrup. dreptunghiulare dacă satisface x = huh (acest termen este folosit uneori într-un sens mai larg, a se vedea [1].).

Semigrupul idempotent

Următoarele condiții pentru semigrup S echivalent: 1) S este dreptunghiular, 2) Sest perfect simplu n IA (vezi semigrup simplă), 3) Sest destul de simplu idempotente semigrup, 4) S este izomorfă produsul direct al LR, unde levosingulyarnaya L- și .. R este o semigroupă drept-singulară. Fiecare I. n. Semigrup este Clifford și în semilattice descompune (a se vedea. Bundle semigrup) de semigrup dreptunghiular. Această descompunere servește drept punct de plecare pentru studierea multor proprietăți ale unui spațiu ideal. Orice spațiu ideal este finit la nivel local.

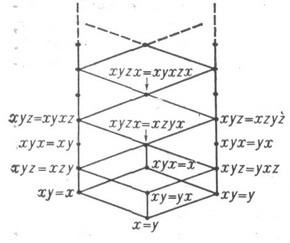
Ele au fost studiate din diferite puncte de vedere, inclusiv din punctul de vedere al teoriei soiurilor. Gridul tuturor subvarietăților din soiul B al tuturor formelor algebrice este descris complet în [4] - [6]; Ea este numărabilă și distributivă, fiecare submanifolă a acesteia poate fi dată într-o singură identitate. Diagrama acestei rețele este prezentată în Fig. În același loc sunt date identități care atribuie colecțiilor mai multor "pardoseli" inferioare.

Lit. : Ll] Clifford A. Preston G. Teoria algebrică a semigrupurilor, trans. cu engleza. t. 1-2, M. 1972; [2] McLean D., "American Math. Monthly", 1954, v. 61, nr. 2, p. 110-13; [3] Kimura N. "Pacif J. Math.", 1958, v. 8, p. 257-75; [4] AP Biryukov, "Algebra și logica", 1970, vol. 9, nr. 255-73; [5J Gerhard J. "J. Algebra", 1970, v. 15, nr. 2, p. 195-224; [6] Fennemore C, "Math. Nachr.", 1971, Bd 48, Nr. 1-6, S. 237-62.

Distribuiți această pagină

  • O BRANDT DE A SEMIGROUP este un semigrup S cu zero, în care fiecare element non-zero corespunde unor astfel de elemente determinate în mod unic. asta. și pentru oricare două idempotenturi nonzero are loc.
  • Gaussian semigrup - semigrup comutativ cu drept unitate de reducere satisfăcătoare, într-un roi orice element ireversibil în produsul arazlozhim elementelor ireductibile, în care are loc pentru oricare două astfel de expansiune, și k = l.
  • O semigrup inversă este un semigrup în care pentru orice element există un element invers unic a -1.
  • Semigrupul local finit este un semigrup în care fiecare subsemigroup finit generat este finit. Fiecare LFC va fi un semigrup periodic. Reversul nu este adevărat: există și periodice. grupuri care nu sunt finite la nivel local.
  • Un semigrup monogonal este o semigrupa ciclică a, este o semigrupă generată de un element. Un spațiu metric generat de un element a este de obicei indicat și constă din toate puterile posibile cu exponenții naturali.
  • O semigroupă nilpotentă este o semigrupă cu zero, pentru care există un n astfel încât.
  • Parametrul semigrup - familia operatorilor care acționează într-un Banach sau topologic spațiu vectorial X, cu proprietatea că în cazul în care operatorii Tlineyny sunt limitate și sunt pe un spațiu Banach X, atunci măsurabilității tuturor.
  • Un SEMIGROUP SIMPLU este un semigrup care nu conține propriile sale idealuri sau congruente de orice tip fix. În funcție de tipul examinat, apar diferite tipuri de tip pi. ideal simplu - nu conține.
  • FREE SEMIGROUP - peste alfabetul A - semigrup, elemente din care. sunt toate posibilele secvențe finite ale elementelor lui A, iar operația constă în atribuirea unei secvențe celeilalte.
  • SEMIGROUPS TOPOLOGICE - set, algebrice alocate. Structura unui semigrup și a structurii topologice Hausdorff. spațiu, iar operația semigrup este continuă într-o topologie dată.
  • Un semigrup ordonat este un semigrup dotat cu o structură de ordin stabil în raport cu o operație semigrup, adică, pentru orice elemente a, b, c, rezultă că. Există o ordine liniară, atunci S este chemată. liniar.
  • Semigrupul este unul dintre conceptele de bază ale algebricii moderne. Un set este numit un set cu o operație definită pe acesta, sub rezerva legii asociativității.

    Marea Enciclopedie Sovietică

  • COMPRESIILE UNUI SEMIGROUP Un semigrup cu un parametru puternic continuu T. T = I, al operatorilor liniari într-un spațiu Banach E pentru care.

    Împreună. Separat. Printr-o cratimă. Glosar Directory

    Dicționar de ortografie rus

    Articole similare

    Pagina anterioară

    Pagina următoare