Examenele de admitere în fizică
III. electrodinamică
1 Două bile mici, dintre care una este inițial în repaus, iar al doilea a avut o anumită viteză, în timp ce prima minge la o distanță mare, mai aproape de distanța L. Știind că direcția celei de a doua viteza mingii au rămas neschimbate, găsi valoarea vitezei v. Influența asupra bilelor tuturor celorlalte corpuri și pierderea de energie a bilelor de pe radiație este neglijată. Masa primei mingi este egală cu m, iar cea de-a doua - M. Încărcarea fiecărei mingi este egală cu q.
Prin condiția problemei, alte organisme nu acționează asupra bilelor. Prin urmare, putem presupune că starea inițială a sistemului constând din bile este dată relativ la observatorul inerțial și acest sistem este izolat. Deoarece direcția celei de a doua viteza mingii rămâne neschimbată, este necesar să se presupună că ambele bile în timpul cursei de abordare de-a lungul unei linii drepte, iar la momentul cel mai apropiat de abordare a vitezei relative a bile este zero, adică Viteza bilelor în acest moment față de observatorul indicat devine egală cu:
Deoarece granulele formează un sistem izolat în care există forță disipativ, în orice moment, inclusiv la momentul cel mai apropiat de abordare a bilelor trebuie efectuate lege de conservare impuls și legea de conservare a energiei:
unde este constanta electrica. La înregistrarea legea de conservare a energiei a fost considerat că bilele se deplasează în mod constant, și pierderea de energie mecanică din cauza radiației în mișcare, cu o accelerare a corpurilor încărcate, cu condiția problemei, ar trebui să fie ignorate.
Rezolvând împreună ecuațiile de mai sus, găsim valoarea dorită a vitezei:
2 pe tija dielectric perle subtiri orizontale netede mici purtând două sarcini + q și -q, capsat între un dielectric rigiditate arc k. Întregul sistem se află într-un câmp electric omogen, ale cărui forțe sunt paralele cu tija. Arcul nu este deformat. Dacă direcția câmpului este inversată, rămânând nemodificată valoarea de intensitate E, lungimea arcului la echilibru se va reduce până la n = 2 ori. Neglijând polarizarea dielectricilor, găsiți valoarea lui E.
Presupunem că tija cu bile și sursa de câmp electric extern este în repaus în raport cu unele sistem de referință inerțial. Apoi, neglijând în conformitate cu condiția problemei forțelor de frecare dintre bile și tija și tija arc și polarizare, se poate argumenta că forțele care acționează asupra bilelor de câmpul electric în orientarea inițială a vectorului intensității câmpului, echilibrată forța de atracție reciprocă de bile, și anume . relația
unde l0 este lungimea arcului nedeformat, este constanta electrica.
După schimbarea direcției vectorului intensității câmpului extern în starea de echilibru final al duratei de primăvară condiției sarcină devine ori mai mică decât originalul n. În consecință, în conformitate cu legile lui Coulomb și Hooke, relația
Substituind în această expresie valoarea qE din ecuația anterioară, constatăm că lungimea arcului în stare nedeformată trebuie să satisfacă relația și valoarea necesară a intensității câmpului este
3 La o distanță de 2R de centrul bilei conductoare fixe cu raza R, se păstrează o sarcină de punct pozitivă de 2Q. taxa mingea este Q. Ce v viteza poate dobândi electroni începe mișcarea sa de la punctul de la infinit, în momentul contactului cu mingea?
În rezolvarea problemei va presupune că mingea revine la un sistem de referință inerțial, se mișcă de electroni în vid și energia electronilor pot fi neglijate pierderile de radiație, adică, vom presupune că accelerația electronului este suficient de mică. Atunci când un electron se apropie mingea din cauza fenomenului de inducție electrostatică ar trebui să fie o redistribuire a glob de încărcare. Presupunem că materialul mingea are o conductivitate suficient de mare, și pierderi de energie, prin urmare, pot fi ignorate cauzate de caldura Joule în timpul fluxului de curent de conducere, și să presupunem că toate punctele de mingea conductive au același potențial, și, prin urmare, întreaga sarcină de exces ca în electrostatics , este distribuită numai pe suprafața sferei.
Fie valoarea încărcăturii situată pe o bucată i-a unei suprafețe suficient de mică a sferei să fie egală cu qi. Prin condiția problemei, mingea este izolată, iar sarcina ei este egală cu Q. Prin urmare, conform legii conservării taxelor și ipotezelor făcute mai sus, în orice moment al timpului, toate piesele de pe suprafața mingii sunt egale cu Q.
Vom presupune, ca de obicei, că potențialul câmpului electrostatic produs de o sarcină staționară q într-un punct infinit de îndepărtat este zero. Apoi, potențialul câmpului electrostatic la o distanță r față de sarcina punctului este cunoscut a fi egal cu
unde este constanta electrica. În conformitate cu principiul suprapunerii, potențialul creat de un sistem de taxe punctuale la un anumit punct este egal cu suma potențialelor create de fiecare dintre aceste taxe separat în acest moment. În consecință, potențialul centrului mingii cu privire la punctul de la infinit îndepărtat de acesta, cauzat de excesul de sarcină al bilei și de încărcarea punctului 20, situat din centrul bilei la o distanță 2R, este egal cu
Conform celor spuse mai sus, același lucru ar trebui să fie potențialul oricărui punct al suprafeței sferei, iar din expresia obținută rezultă că acest potențial nu depinde de poziția electronului. Prin urmare, atunci când ipotezele formulate mai sus, forța de muncă a câmpului electrostatic generat de taxa de bilă și 2Q de încărcare, se deplasează peste electronul câmp nu depinde de tipul traiectoriei de electroni și este determinată numai de pozițiile sale inițiale și finale. Deoarece încărcarea unui electron este negativă, acest câmp în cursul mișcării electronului către minge va efectua o lucrare pozitivă asupra electronului unde este modulul de încărcare a electronului. Prin urmare, în conformitate cu legea schimbării energiei cinetice, rezultă că valoarea dorită a masa m a vitezei electronilor atunci când este plasat pe suprafața bilei în vedere pierderea de energie a electronilor din cauza radiației și căldură Joule în minge trebuie să satisfacă inegalitatea
4 În circuitul prezentat în Fig. 1, printr-o rezistență R1 = 15 ohmi curg curent I = 10A, a căror valoare nu depinde de poziția R. reostat motorului Găsiți bateriile electromotor vigoare în acest sistem, în cazul în care r1 rezistență internă prima baterie = 5 ohmi.
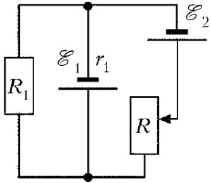
La rezolvarea problemei, vom neglija, ca de obicei, rezistența firelor și a contactelor între elementele circuitului. Deoarece rezistorul R1. prima baterie și a doua baterie împreună cu reostatul R sunt conectate în paralel, căderea de tensiune pe rezistența R1 a primei baterii și pe a doua baterie cu reostatul R trebuie să fie aceeași. Fie suma rezistenței interne a celei de-a doua baterii și cea a reostatului R inclusă în circuit să fie r2. Apoi, conform legii lui Ohm și a celor de mai sus, trebuie îndeplinite următoarele relații:
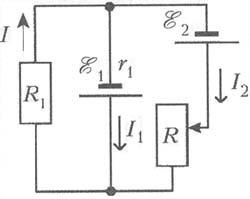
La scrierea acestor relații, sa presupus că direcțiile curenților din ramificațiile circuitului corespund săgeților arătate în Fig. 2. În virtutea legii conservării încărcării și a constantității curenților în ramificațiile circuitului pentru direcțiile indicate de curenți, valorile lor trebuie să satisfacă relația I = I1 + I2. și prin urmare curentul prin rezistorul R1 trebuie să satisfacă ecuația
Această ecuație este o identitate pentru orice r2. dacă = IR1 (adică, I2 = 0) și = I (R1 + r1). Astfel, valorile EMF necesare sunt egale:
5 Pe două pneuri paralele, fixate la un unghi de 45 ° față de orizont, o punte poate aluneca, rămânând perpendiculară pe ea. Autobuzele sunt interconectate printr-un conductor fix. Rezistența jumperului este mult mai mare decât rezistența anvelopelor și a conductorului. Întregul sistem se află într-un câmp magnetic uniform, a cărui inducție B este perpendiculară pe planul anvelopei. Dacă direcția câmpului magnetic este verticală, fără a schimba valoarea lui B, atunci viteza constantă a podului va fi diferită în k = de 0,8 ori față de cea observată anterior. Neglijând inductanța circuitului conductor, găsiți coeficientul de frecare al podului în jurul magistralei.
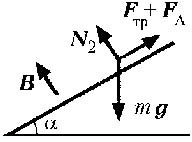
La rezolvarea problemei, presupunem că autobuzele și conductorul care le conectează sunt fixate împreună cu sursa câmpului magnetic relativ la sistemul de referință de laborator și acest sistem este inerțial. Atunci când jumperul se mișcă, fluxul câmpului magnetic cuplat la circuitul conductorului format de pod, autobuzele și conductorul de legătură se vor schimba. Prin urmare, în acest circuit trebuie să apară un curent de inducție, a cărui direcție, conform regulii Lenz, trebuie să fie astfel încât mișcarea punții să fie decelerată. Pentru a frâna mișcarea jumperului vor exista forțe de frecare care acționează asupra jumperului de pe partea pneului. Prin urmare, puntea în starea de echilibru poate să alunece numai pe autobuze. Având în vedere acest lucru, Fig. 3 arată forțele care acționează asupra barei de bare alunecând în jos pe barele magistrale atunci când vectorul de inducție B al câmpului magnetic extern este direcționat perpendicular pe barele magistralei. Aici mg este forța gravitației, m este masa podului și g este accelerația datorată gravitației. Rezistența reacției pneului prezentată în figură, sub forma a două componente: normal N și tangențiale FTR, numit de obicei uscat de alunecare forță de frecare, valoarea care, potrivit Coulomb-lege Amontons egal cu N. In final, FA - Amperi. Conform legii lui Ampere, această forță este direcționată perpendicular pe vectorul B al inducției câmpului magnetic și podului, adică paralel cu anvelopele și din două direcții posibile este ales cel care, așa cum sa menționat mai sus, este în concordanță cu regula Lenz. Din ceea ce sa spus și al celei de-a doua lege a lui Newton rezultă că ecuația de mișcare a podului în proiecție pe axa paralelă cu autobuzele este de forma
unde a este proiecția accelerației podului pe direcția indicată.
Deoarece podul se deplasează de-a lungul anvelopei, componenta normală a forței de reacție a anvelopei N = mg cos. Dacă distanța dintre autobuzele notate L, și punte de rezistență R, atunci, în conformitate cu regula fluxului Faraday-Maxwell și legea lui Ohm, curentul care trece prin pod în timpul valorii vitezei de circulație egală cu 1. trebuie să fie egal cu I1 = BL1 / R, m. a. cu privire la sarcinile de condiție de rezistență și alte elemente ale circuitului care efectuează și inductanța ar trebui să fie ignorate. Având în vedere că câmpul magnetic sunt reciproc perpendiculare și pe web, valoarea forței găsi Ampere și apoi obține ecuațiile de mișcare a care în pânze de mișcare constantă (adică, atunci când a = 0), amplitudinea vitezei sale
În cazul în care un câmp magnetic extern este direcționat vertical care acționează asupra săritor forței Ampere orientată în direcție orizontală, în mod convenabil reprezentat în forma a două componente, dintre care una este paralelă cu șinele, iar celălalt - perpendicular pe ele, așa cum se arată în Fig. 4. repetând aproape literal raționamentul de mai sus, se poate demonstra că viteza benzilor de 2 prin curent de legătură trebuie să curgă Amperi Astfel, aceste componente de forță va fi egală cu
iar ecuația de mișcare a podului în proiecție pe axa paralelă cu autobuzele va avea forma unde
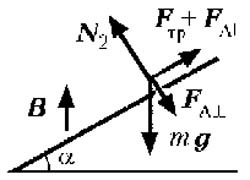
În consecință, în acest caz, valoarea vitezei la starea de echilibru a podului atunci când ipotezele făcute sunt
Dacă, de obicei, presupunem că coeficientul de frecare nu depășește unitatea, atunci rezultă din expresiile obținute că, prin urmare, în funcție de condiția problemei, coeficientul de frecare necesar
Dacă, pe de altă parte, presupunem că coeficientul de frecare depășește unitatea, care de regulă nu are loc, cantitatea necesară trebuie să fie egală cu
Continuare în nr. 18