Figura 16 - Graficul funcției F (x) a distribuției uniforme
Asteptarea matematica a unei variabile aleatoare X. distribuita printr-o lege uniforma pe o sectiune [a. b], după cum rezultă din interpretarea mecanică (centrul de masă), este egală cu abscisa din mijlocul secțiunii: M [X] = (a + b) / 2. Același rezultat poate fi obținut și calculul integralului:
varianța variabila aleatoare X poate fi găsită, bazată pe interpretarea mecanică (momentul inerțial al distribuției în raport cu centrul de masă): D [X] = (b - a) 2/12. Acelasi rezultat poate fi obtinut prin calcularea integrala:
Abaterea medie pătrată a unei variabile aleatorii distribuite uniform
Modurile nu au o distribuție uniformă; media lui din considerente de simetrie este (a + b) / 2. Din aceleași motive de simetrie asimetria A [X] = 0. Coeficientul de aplatizării al unei variabile aleatoare X este egal cu -1.2: Ex [X] = -1.2; așa cum era de așteptat, este negativ.
Un exemplu de o variabilă aleatoare care are o lege de distribuție uniformă, un timp de așteptare de evenimente regulate, cum ar fi timpul de așteptare în tren de metrou, de așteptare pentru stația de autobuz pe o anumită rută.
Să luăm în considerare câteva exemple de variabile aleatorii având o distribuție uniformă. Atunci când se măsoară o anumită valoare cu un dispozitiv la scară largă, erorile de rotunjire sunt distribuite conform unei legi uniforme. Evident, erorile care rezultă din rotunjirea datelor în calcule au o distribuție uniformă.
Exemplul 17 Trenurile de metrou rulează la intervale de 4 minute. Pasagerul ajunge în orice moment la platforma trenului. Găsiți probabilitatea ca el să aștepte trenul să ajungă cel mult un minut. Găsiți timpul mediu de așteptare pentru tren de către pasageri, calculați varianța și abaterea standard a timpului de așteptare pentru tren de către pasageri.
Soluția. Luați în considerare variabila aleatoare X - timpul în care pasagerul așteaptă trenul. Toate valorile posibile ale unei variabile aleatorii date aparțin intervalului [0; 4] și, conform condiției, toate aceste valori sunt la fel de posibile. În consecință, variabila aleatoare este distribuită conform unei legi uniforme cu parametrii a = 0 și b = 4. Funcția de densitate de probabilitate a unei variabile aleatorii date:
Să găsim probabilitatea ca un pasager să aștepte un tren nu mai mult de un minut:
În figura 17, o figură este selectată cu ecloziune, a cărei suprafață este egală cu probabilitatea
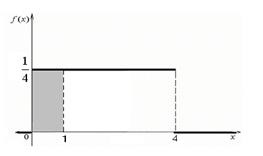
Figura 17 - Graficul densității de distribuție a probabilității
valoarea aleatorie X - timpul de așteptare pentru trenul de călători
Durata medie de așteptare pentru sosirea trenului de către pasager