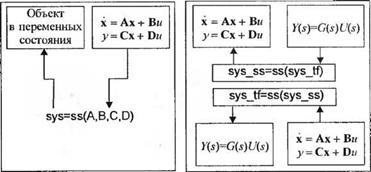
Analiza sistemelor de control în domeniul timpului presupune asignarea modelului său în spațiul de stări:
x = Ax + Brz și y = Cx + Da. (3.127)
Caracterizează vectorul x stare al matricei sistemului A este o matrice coeficient de nxn dimensiuni, B - intrare matrice dimensiune n x, C - o dimensiune PXn ieșire matrice, D - parcurgeri matrice dimensiune RCT. Noi ne limităm la ASIC cu o singură intrare și o ieșire, deci în acest caz m - p = 1, și a_u g / Xia sunt variabile scalare (bold care nu sunt utilizate pentru ele).
Elementele de bază ale modelului în spațiul de stare (ZI27) sunt vectorul x și matricea (A, B, C, D). O astfel de descriere este cea mai potrivită pentru utilizarea mediului MATLAB, în care unitatea principală de lucru este o matrice. De fapt, MATLAB acoperă atât de multe metode diferite bazate pe spațiul statelor, încât pur și simplu nu le putem considera pe toate. În această secțiune, vom introduce două noi funcții: ss și Isim. În plus, considerăm funcția expT, prin care se calculează matricea de stare de tranziție.
Dacă este dată o funcție de transfer, atunci putem obține un model echivalent al sistemului în variabilele de stare și invers. În acest scop, MATLAB are două funcții: funcția ss permite trecerea de la funcția de transfer la reprezentarea sistemului în spațiul de stare, funcția tf efectuează problema inversă. Semnificația acestor funcții este prezentată în Fig. 3,28.
De exemplu, luați în considerare un sistem de ordinul trei:
R (s) s - i 2 + 1 b-V + 6