Viscozitatea unui lichid poate fi definită ca rezistența unui lichid la mișcarea unui strat față de celălalt. Orice mișcare a unei părți a fluidului în raport cu cealaltă este inhibată de forțele de atracție dintre elementele sale. Cu alte cuvinte, viscozitatea unui lichid caracterizează frecarea internă care apare atunci când straturile de fluid se deplasează unul față de celălalt.
Bazele teoriei vâscozității. În analiza teoretică a viscozității, lichidul este reprezentat ca un mediu continuu nestructurat. Dacă aplicați forța unui lichid, acesta începe să curgă. Fluidele sunt caracterizate de două tipuri principale de flux: laminar și turbulent.
Debitul laminar se numește fluid sub formă de straturi paralele care nu se amestecă între ele. Un astfel de flux există până când mărimea gradientului de viteză este prea mare. Pe măsură ce crește gradientul de viteză, straturile de fluid formează vîrtej și se amestecă. În astfel de cazuri, fluxul laminar devine turbulent și situația este dificil de interpretat atât teoretic, cât și experimental. Legile de vâscozitate considerate de noi se vor referi doar la regimul fluxului laminar.
Să luăm în considerare două elemente de volum adiacente ale unor lichide. În cazul în care una dintre ele este deplasat în raport cu celălalt cu o forță externă, între ele tam-tam-cabine forțele care vor preveni astfel de deplasări-Niju, încercând să se întoarcă elementele de volum în poziția lor de echilibru. Această forță de interferență (F) este numită forța de frecare internă (rezistență).
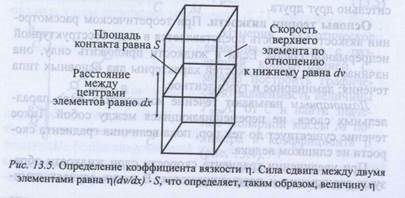
Pentru a determina cantitativ vâscozitatea, putem folosi Fig. Să presupunem că unul dintre elementele volumetrice ale lichidului reprezentat în această figură se mișcă cu viteza dv față de al doilea element. Se poate aștepta ca forța de frecare să fie proporțională cu viteza relativă dv și zona de contact S între elementele de volum adiacente. Acesta va fi invers proporțional cu distanța dx dintre centrele acestor elemente. Constanta proporționalității care corelează forța de frecare și variabilele date se numește coeficientul de vâscozitate sau pur și simplu vâscozitatea # 942; |. Denotând forța de frecare cu F, obținem:
Această definiție a viscozității inițial a fost dată de Newton. Este microscopică, exprimată prin cantități care nu pot fi măsurate.
Unitatea de vâscozitate este de secunde newton pe metru pătrat (N # 8729; s / m 2) sau Pascal secunde (Pa # 8729; s); mai devreme pentru o unitate de vâscozitate, sa luat o poise:
1 poise = 0,1 Pa # 8729;
Caracteristicile vâscozității soluțiilor polimerice. Coeficient de viscozitate # 946; nu depinde de presiunea aplicată, nici de gradientul de viteză (în condiții de flux laminar uniform).
Osul lichid, care respectă legea lui Newton, se numește Newtonian. Soluțiile IUD nu sunt de natură vâscozitate # 942; depinde de gradientul de viteză. De fapt, pentru soluțiile marinei, fenomenul fluxului determină orientarea macromoleculelor dizolvate (figura 6).
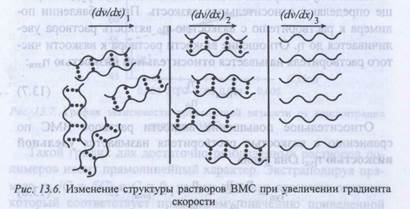
Odată cu creșterea vitezei de gradient entiruyutsya-macromoleculă de-a lungul ori axa de curgere și, prin urmare, viscozitatea soluției scade DIU, și pentru anumite valori ale gradientul vitezei structurilor supramoleculare se poate prăbuși, după care soluția dobândește proprietățile unui fluid Newtonian. Lichidele care prezintă efecte similare de direcționare sunt numite non-newtoniene.
Vâscozitatea soluțiilor conținând macromoleculei polimer, în mod tipic soluții de vâscozitate mult mai mare de compuși cu greutate moleculară mică și soluții coloidale de aceleași concentrații. Prin urmare, numai soluțiile foarte diluate de IMS în condiții de flux laminar pot fi considerate newtoniene.
Creșterea vâscozității soluției de polimer în comparație cu viscozitatea solventului se datorează nu numai concentrației sale, ci și unui număr de parametri ai macromoleculei.
Astfel de parametri sunt:
1. volumul soluției ocupate de macromolecule (volum specific);
2. raportul dintre lungimea moleculei și lățimea acesteia (raportul axial);
3. Rigiditatea moleculei.
Pentru moleculele globulare, care sunt moleculele multor proteine, volumul molecular este de importanță fundamentală. Acesta poate fi ușor legat de greutatea moleculară relativă. În cazul moleculelor subțiri foarte dure, cum ar fi ADN-ul, efectul principal este asigurat de raportul axial; este de asemenea o funcție a greutății moleculare relative. Dacă este cunoscută masa moleculară relativă, atunci se poate obține informații despre forma generală a moleculei.
Deoarece măsurătorile absolute ale vâscozității sunt dificile, este adesea determinată vâscozitatea relativă. Când se adaugă un dimer la un solvent cu vâscozitate O viscozitatea soluției este mărită la # 942; Raportul dintre vâscozitatea soluției și viscozitatea unui solvent pur se numește viscozitatea relativă # 942;
Creșterea relativă a vâscozității soluției IUS în comparație cu viscozitatea solventului se numește vâscozitatea specifică # 942; Este egal cu
Viscozitățile relative și specifice sunt cantități fără dimensiuni și depind de concentrația polimerului. Dar ei nu pot fi direct legate de parametrii macro-molecule (de exemplu, forma și mărimea acesteia), astfel au fost introduse conceptul de mai sus și caracteristice vâsco pereților.
Viscozitatea specifică pe concentrație de unitate se numește viscozitatea redusă
unde C este concentrația masică a polimerului, g / cm3.
Valoarea limită a vâscozității reduse într-o soluție infinit diluată se numește viscozitate internă sau caracteristică [# 942;]:
Se determină experimental prin plotarea dependenței vâscozității reduse UD / C din diferite concentrații ale polimerului (figura 7).
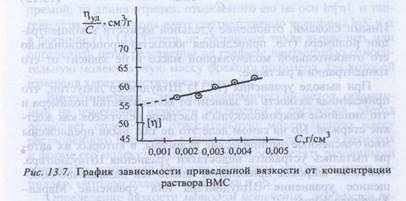
Un astfel de grafic pentru soluții destul de dilatate ale limitelor este de natură directă. Extrapolând drept # 942; sp / C = / C) la C = O, ordonatei, care corespunde valorii de limitare a viscozității reduse, adică din viscozitatea intrinsecă [# 942;].
Viscozitățile reduse și caracteristice au dimensiuni, concentrații inverse, adică cm3 / g.
Viscozitatea intrinsecă depinde moleculare relativ greutatea, forma și volumul specific al unui macromolecular-Kula, capacitatea sa de a schimba forma în funcție de solventul sub tije (schimbare conformationala), dar nu depinde de concentrația polimerului în soluție și rata reciproc imnogo se deplasează straturi lichide.
Relația dintre vâscozitatea intrinsecă și greutatea moleculară relativă a polimerului.
Staudinger a propus o formulă pentru determinarea masei moleculare relative a DIU:
unde Vg este vâscozitatea specifică a soluției; K este o constantă, cm3 / g; M este greutatea moleculară relativă a IUS; C - concentrația IUS în soluție, g / cm3.
Din ecuația rezultă: # 942; UD / C = KM
Raportul dintre viscozitatea specifică până la atingerea concentrației polimerului (adică, viscozitatea redusă) proporțională cu greutatea sa moleculară relativă și nu depinde de concentrația sa în soluție.
În ecuația derivă Staudinger presupus că vâscozitatea redusă este independentă de concentrația polimerului și că macromoleculele liniare în soluție ca să se comporte tije gest-Kie. Dar, de fapt, nu este. S-a propus numeroase formulă empirică, în care ecuația lor de auto-riu Staudinger a încercat să elimine dezavantajele. Cel mai frecvent utilizat este așa-numita ecuație generalizată Staudinger-Hailey Mark-Hauwink-Kuhn:
unde K și # 945; - constante pentru o serie omologă polimer dată și un solvent dat.
Aceste constante sunt în general determinate empiric pentru fiecare sistem de solvent“- solute„folosind compus cunoscut în raport clorhidric-greutate moleculară, deoarece nu există încă nici o teorie adecvată pentru calcularea acestora. Constantele K și # 945; definit pentru acest sistem "polimer-solvent", nu poate fi utilizat pentru alt sistem.
Constanta K are o valoare de ordinul 10-4. Pentru macromoleculele tari # 945; ≈1, pentru moleculele polimerice flexibile care aproximează forma în sferă, # 945; ≈ 0,5, în timp ce pentru polielectroliți foarte încărcați # 945; ≈2.
Dependența (13.13) poate fi scrisă și în forma ln [# 942;] = lnK + # 945;
Această ecuație este ecuația unei linii drepte în coordonatele lnM, ln [# 942;]. Prin măsurarea viscozității intrinseci cât de multe produse non-standard cu cunoscute moleculare mase-TION relativă și plasată într-un punct corespunzător de coordonate LPM, Ln [# 942] (. Figura 8), este posibil să se verifice valabilitatea (13,14), în acest caz. Dacă punctele reprezentate pe grafic se află de fapt pe aceeași linie dreaptă, atunci lungimea segmentului tăiat de ea pe axa ln [# 942;] și tangenta unghiului # 946; Panta sa este dată de cantitățile lnK și # 945; în formula (13.14). Acum nu este dificil să se calculeze sau să se determine direct pe grafic greutatea moleculară relativă necunoscută a fracțiunii polimerice pentru care se măsoară viscozitatea intrinsecă.

