Declarația problemei: Despre un cerc a cărui rază este R, descriem un poligon al cărui domeniu este egal cu S. Găsiți perimetrul acestuia.
Problema face parte din USE privind matematica nivelului de bază pentru clasa 11 la numărul 15 (Probleme de planificare).
Să analizăm modul în care aceste probleme sunt rezolvate utilizând exemplul și derivă o soluție generală.
Lângă un cerc a cărui rază este de 3, vom descrie un poligon a cărui suprafață este de 33. Găsiți perimetrul său.
Pentru a rezolva această problemă, conectăm centrul cercului cu toate vârfurile poligonului și tragem înălțimile în triunghiurile rezultate în părțile laterale ale poligonului.
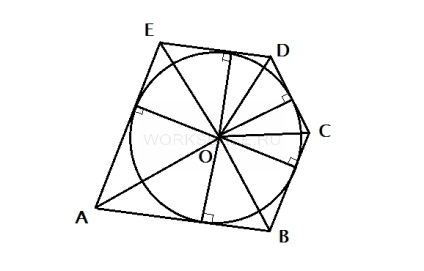
Pentru a obține zona poligonului, obținem zonele celor 5 triunghiuri și le adăugăm. Rețineți că înălțimea fiecărui triunghi este egală cu raza cercului.
SABCDE = 1/2 ⋅ R ⋅ (AB + BC + CD + DE + EA)
Rețineți că suma lungimilor tuturor laturilor, adică a perimetrului P, este obținută în paranteze. Prin urmare, puteți converti zona poligonului în următoarea formă:
SABCDE = 1/2 ⋅ R ⋅ P
Rămâne să înlocuiți valorile specifice și să exprimați perimetrul:
P = 33/3 ⋅ 2 = 22
Astfel, perimetrul poligonului este 22.
În general, soluția la această problemă în planimetrie este după cum urmează:
PERIMETRUL unui poligon = 2 ⋅ S / R
unde S este zona poligonului și R este raza cercului înscris în el.
Rămâne doar să înlocuiți valorile specifice și să calculați rezultatul.