Funcțiile sunt infinitezimale dacă, în timp ce x tinde la punctul a, limita lor este 0.
Cu toate acestea, o funcție infinitezimală poate exista doar la un anumit punct. După cum se arată în figura 1, funcția este infinitezimală numai la punctul 0.
Figura 1. Funcție infinit de mică
Dacă limita coeficientului a două funcții dă 1 ca rezultat, funcțiile se consideră a fi echivalente cu infinitesimal ca x tinde la a.
Dacă funcțiile f (x), g (x) sunt infinitezimale pentru $ x> a $, atunci:
- Funcția f (x) se numește o infima de ordin superior în ceea ce privește g (x), în cazul în care condiția: \ [\ mathop \ limits_ \ frac = 0 \]
- f (x) funcția se numește ordine infinitezimal n-lea în ceea ce privește g (x), dacă este diferit de 0 și limita finit: \ [\ mathop \ limits_ \ frac (x)> = A \]
Funcția $ y = x ^ 3 $ este o infima de ordin superior pentru x> 0, în comparație cu funcția y = 5x, deoarece limita relației lor este egală cu 0, acest lucru se explică prin faptul că funcția $ y = x ^ 3 $ tinde la zero Valoare mai rapidă:
Funcțiile y = x2-4 și y = x2-5x + 6 sunt infinit de mici de aceeași ordine pentru x> 2, deoarece limita raportului lor nu este 0:
Proprietăți de infinitezimale echivalente
- Diferența a două infinitezime echivalente este infinitezimală de ordin superior în raport cu fiecare dintre ele.
- În cazul în care suma mai multor ordine diferite de infinitezimal picătură infinitezimal de ordin superior, partea rămasă, numită comitent, este echivalentă cu întreaga sumă.
Din prima proprietate rezultă că infiniteimalele echivalente pot deveni aproximativ egale cu o eroare relativ mică, arbitrar. Prin urmare, semnul ≈ este utilizat atât pentru a denota echivalența infinitului cât și pentru a scrie egalitatea aproximativă a valorilor lor suficient de mici.
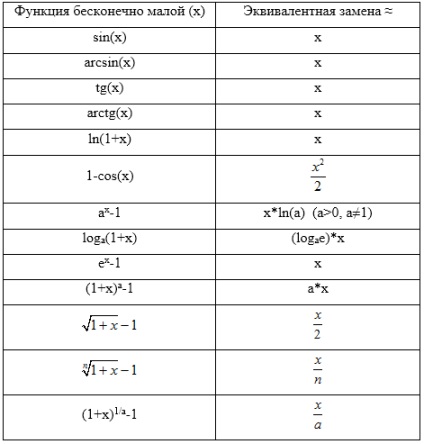
Atunci când găsiți limite, este adesea necesar să utilizați înlocuirea funcțiilor echivalente pentru viteza și comoditatea calculelor. Tabelul cu infiniteimali echivalenți este prezentat mai jos (Tabelul 1).
Echivalența infinitezimilor date în tabel poate fi dovedită pe baza egalității:
Înlocuirea valorilor echivalente