Unele S nu sunt P.
va apărea în următoarea formă:
├.
În mod similar, putem să scriem restul sylogismelor: atât imediate, cât și indirecte.
§ 4. Metode de verificare a corectitudinii silogismelor
Sarcina logicii este de a separa raționamentul corect de cel rău. În mod firesc, aceeași sarcină trebuie rezolvată în ceea ce privește silogismul. Practic, toate argumentele date mai devreme (cu excepția exemplului raționamentului din dialogul din secțiunea 1 a acestui capitol) sunt corecte. Dar, din practica comunicării noastre zilnice, știm că, de fapt, raționamentul incorect apare destul de des. Se pune problema: cum să criticați raționamentul greșit? Această sarcină este rezolvată prin modalități de a verifica corectitudinea silogismelor.
Există trei astfel de metode:
1) construirea schemelor circulare pentru parcele și încheierea silogismelor;
2) prezentarea unui exemplar contrar;
3) verificarea conformității cu regulile generale ale silogismelor și regulilor cifrelor.
Să luăm în considerare aceste metode separat.
1) Construirea circuitelor circulare pentru colete și combinarea acestora pe aceeași schemă.
Acesta este cel mai simplu mod de a verifica. În silogismul potrivit, combinația schemelor circulare construite pentru fiecare spațiu trebuie să ducă la un rezultat clar, care coincide cu relația dintre termenul mai mic și cel mai mare în concluzie.
Toți avocații cunosc semnele unei crime.
Nici unul dintre cei prezenți nu cunoaște semnele unei crime.
Nici unul dintre cei prezenți nu este un avocat.
Aceasta este a doua cifră, modul AEE.
Denumiți termenii: "avocat" - prin P. "O persoană care știe semnele unei crime" - prin. "Prezent" prin S. Apoi pentru o premisă mai mare obținem următoarea schemă:
Pentru cea de-a doua premisă, respectiv următoarea schemă:
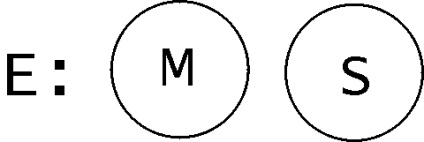
Combinația acestor scheme va da următorul rezultat:
Vedem că nu poate exista altă relație între S și P. și anume am obținut un rezultat unic. Concluzia noastră "Nimeni nu este P" în acest sistem este adevărat. Aceasta înseamnă că, cu adevărul premiselor, concluzia este în mod necesar adevărată, ceea ce înseamnă că concluzia inițială este corectă.
Toți avocații cunosc semnele unei crime.
Toți cei prezenți cunosc semnele de infracțiune.
Toți cei prezenți sunt avocați.
Aceasta este și a doua cifră, moda AAA. Indicați termenii silogismului în același mod ca și în exemplul anterior. Apoi, pentru o premisă mai mare, se obține o schemă, ca în exemplul precedent.
Pentru o premisă mai mică, se obține următoarea schemă:
Combinăm aceste scheme într-o schemă circulară:
Vedem că aceste scheme pot fi combinate în moduri diferite. și anume nu am obținut un rezultat clar. Și pe schema combinată (a) concluzia noastră este adevărată, dar pe schema combinată (b) concluzia noastră este falsă. Cum să interpretăm rezultatele combinației noastre de scheme circulare pentru parcele? Reamintim că, în premisa dreaptă a raționamentului deductiv și concluzia trebuie să fie în ceea ce privește consecința logică. În același timp, știm că nu există nici o relație de consecință logică în cazul în care parcelele pot fi adevărate și concluzia falsă. (Amintiți-vă relația noastră între judecăți complexe!) Aceste relații se poate deplasa pe un model circular de combinații și spun că, dacă există un local diagrame combinate sunt adevărate și concluzia este falsă, atunci silogism noastră nu este corectă. În cazul nostru, există o astfel de schemă - aceasta este schema (b). În consecință, silogismul nostru este greșit.
Prin urmare, putem obține un criteriu general pentru corectitudinea silogismelor:
Syllogismul este corect dacă nu se poate construi o schemă circulară combinată, pe care ambele premise sunt adevărate, iar concluzia este falsă.
De aici rezultă criteriul incorectitudinii silogismelor:
Silogismul este greșit dacă este posibil să se construiască o astfel de schemă circulară, pe care ambele premise sunt adevărate, iar concluzia este falsă.
Un exemplu. Vom aplica metoda dezvoltată pentru discutarea raționamentului despre spartani și a contribuției lor la filosofie, care a lovit personajele dialogului nostru în § 1 din acest capitol. Hai să jucăm ultima dintre silogismele discutate acolo.
Unii greci antice au contribuit la dezvoltarea filosofiei.
Toți spartanii sunt greci vechi.
Unii spartani au contribuit la dezvoltarea filosofiei.
Aceasta este prima cifră, modul IAI. Denumiți un termen mai mare - "cei care au contribuit la dezvoltarea filosofiei" - prin P. mijlocul "grecilor antice" - prin. și mai mici - "Spartans" - prin S. Apoi schema circulară corespunzătoare premisei mai mari va arăta astfel:
ci o schemă circulară care corespunde unei premise mai mici:
Prin combinarea lor, obținem:
În această diagramă, concluzia "Unii Spartani au contribuit la dezvoltarea filosofiei" - fals și ambele premise sunt adevărate. În consecință, se poate construi o astfel de schemă combinată, în care premisele sunt adevărate, iar concluzia este falsă și, prin urmare, raționamentul este incorect.
Explicație. Construcția schemelor circulare nu este un argument într-o dispută. Este puțin probabil să fiți capabil să convingeți pe cineva despre corectitudinea lor, dacă desenați o schemă. Cu toate acestea, ele vor ajuta să înțeleagă situația, pentru a înțelege ceea ce este greșit în argumentul adversarului tău, și să-l întreb, de exemplu, întrebarea: „Sunteți sigur că spartanii sunt tocmai acei greci care au contribuit la filozofia? Dar nu poate fi vorba despre faptul că sunt doar printre aceia dintre grecii care nu au contribuit la filozofie? "Și acum, să încerce să răspundă la întrebările dvs. mai mult sau mai puțin convingător. Inițiativa ți-a fost transferată. O să formuleze întrebări, care sunt o rușine pentru adversarul, aceasta ne-a ajutat un model circular, care arată în mod clar că este necesar să se ceară.
2) Prezentarea unui exemplar contrare.
Modul de a detecta inexactitatea inferențelor prin construirea schemelor circulare încă nu conduce la o victorie convingătoare în discuție. Dimpotrivă, este de natură teoretică. Cum puteți respinge concluziile în practică, astfel încât concluzia greșită a adversarului dvs. să fie foarte evidentă și astfel să vă asigurați că veți câștiga disputa? În acest scop, este adecvat un exemplar contrare.
Counterexample este un silogism identic cu cel dat în formă (adică are aceeași figură și același mod), dar absurd în sens.
Ce înseamnă "absurd în sensul"? Acest lucru înseamnă că parcelele ar trebui să fie evident adevărat judecată contraexemplu, și zaklyuchenieochevidno fals. Acest lucru dă impresia unei absurdități de inferență. Baza metodei de contraexemplul trăiește în inimile noastre pentru o serie de concluzii bune: în ele adevărul spațiilor trebuie să fie sigur să urmeze adevărul concluziei, și în cazul în care concluzia (dacă premise adevărate) în mod evident false, este sentimentul nostru indignat și argumentează împotriva acestei concluzii.
În legătură cu inferența spartanilor și a filosofiei, problema de a găsi și de a prezenta un contra-exemplar este rezolvată după cum urmează. Căutăm o concluzie cu privire la prima figură, modul IAI. Acest mod, după cum știm acum, nu este printre cele corecte. Totuși, trebuie să demonstrăm acest lucru publicului. După cum arată schema circulară construită anterior, trebuie să găsim astfel de concepte de M și P. care ar fi în legătură cu traversarea și un astfel de concept. a căror volum ar fi în mod evident exclus din domeniul de aplicare al conceptului. E nevoie de ceva creativitate. Dar, cel puțin, schemele circulare arată ce să caute. Să luăm ca termeni ai contra-exemplului "poporul", "cei care pot purta copii" și, respectiv, "bărbații". Apoi avem urmatoarea inferenta:
Unii oameni pot rmzhat copii.
Unii bărbați pot da naștere copiilor.
Această deducere este un exemplu. pentru că are exact aceeași formă ca și concluzia despre spartani și filozofie, premisele sale sunt în mod evident adevărate, iar concluzia este și mai evidentă falsă. Mai mult, dacă o astfel de situație se întâlnește într-o discuție reală, acest contra-exemplu ar avea de asemenea un efect comic, iar adversarul tău va fi în cele din urmă ucis.
Pentru un silogism vorbind despre avocați și semne de iluzie, se poate construi următorul exemplu (mai serios):
Toți oamenii stupid trebuie să se supună legii.
Toți oamenii inteligenți trebuie să respecte legea.
Toți oamenii inteligenți sunt proști.
Construind un exemplar contrar, ar trebui să ne adresăm oponentului nostru cu privire la următorul discurs: "Argumentarea dvs. este lipsită de valoare, deoarece, urmând logica voastră, se poate construi un astfel de raționament" și apoi se dă exemplul dvs.
3) Verificați respectarea regulilor generale ale silogismului și a regulilor cifrelor.
Pentru a rezolva problema separării silogismelor drepte de logica greșită, au fost formulate reguli speciale. Încălcarea a cel puțin uneia dintre aceste reguli conduce la incorectitatea silogismului, conformitatea cu toate regulile sugerează că silogismul este corect.
Regulile silogismelor sunt împărțite în reguli ale termenilor și regulilor cifrelor.
PT1. În orice silogism trebuie să existe exact trei termeni.
Un exemplu. Luați în considerare silogismul:
Orice căutarea adevărului merită respect.
Toată știința este căutarea adevărului.
Fiecare știință merită respect.
A se vedea că există exact trei termeni: "căutarea adevărului", "ceea ce este demn de respect", "știința". Așadar, a apărut un silogism.
Toate boxele sunt zadarnice.
Cicero era consulul Romei.
Din aceste premise este imposibil să tragem o concluzie, deoarece există patru termeni și, prin urmare, nu există un termen mediu care să lege parcelele și să permită tragerea concluziei. Deși, desigur, și pentru noi înșine, presupunem că Cicero era un orator, dar cu o conștiință clară nu putem trage concluzii până când nu este clar afirmat.
Uneori există patru termeni în silogism, deși la prima vedere se pare că există doar trei. Aceasta se poate datora, de exemplu, unei omonimii.
Bow este arma sălbatică.
Această plantă este un arc.
Această plantă este arma sălbatică.
Este evident că aici doi termeni sunt ascunși sub un singur cuvânt "arc".
Încălzind această regulă, este conectată eroarea "cvadruplează termenii". Exemple de eroare pe care tocmai am analizat-o.
MT2. Termenul mediu ar trebui să fie distribuit cel puțin într-una din parcele.
Nrimer. Să luăm în considerare concluzia despre știință din PT1. În ea termenul de mijloc "căutarea adevărului" este distribuit într-o premisă mai mare.
Toate lucrările literaturii clasice sunt fascinante.
Unii detectivi sunt fascinați.
Unii detectivi sunt opere de literatură clasică.
Concluzia nu rezultă din premisă, deoarece "munca fascinantă" din mijlocul termenului nu este distribuită în niciun loc, deși este adevărat că unii detectivi sunt opere ale literaturii clasice. Suficient pentru a explica, de exemplu, "Crima și pedeapsa" de Fyodor Dostoievski. Cu toate acestea, acest lucru nu face ca inferența de mai sus să fie corectă.
PT3. Termenul distribuit în custodie trebuie să fie distribuit în parcelă.
Un exemplu. În silogismul PT1, termenul "știință" este distribuit în concluzie, dar este distribuit într-o premisă mai mică.
Toți adevărații filozofi sunt imparțiali.
Nici un politician nu este un adevărat filosof.
Nici un politician nu este imparțial.
În acest exemplu, termenul "persoană imparțială" este distribuit în concluzie și nu este distribuit în parcelă. Și, deși concluzia de aici, cel mai probabil, este adevărată, toate inferențele sunt greșite.
PP2. Din două hotărâri negative, nu se poate trage concluzia.
Un exemplu. Din parcele:
Nici un avocat nu este imparțial.
Nici un istoric nu este imparțial.
Nu se poate deduce nimic despre interogarea termenilor "istoric" și "avocat".
FG3. Concluzia este negativă, dacă și numai dacă una dintre premise este negativă.
Această regulă este evidentă.
PP4. Este imposibil de dedus orice concluzie din două hotărâri speciale.
Un exemplu. Din hotărârile judecătorești:
Unii artiști merită admirație.
Unii moderniști sunt artiști.
Nu puteți deduce nici o concluzie.
PP5. Dacă una dintre premise este o propunere privată, atunci concluzia trebuie să fie și privată.
Această regulă este, de asemenea, evidentă.
Cu ajutorul acestor opt reguli, putem selecta cele corecte din cele 256 de moduri ale silogismului.
Cu toate acestea, în logică s-au elaborat și reguli pentru cifre, astfel încât, în cazul fiecărei figuri individuale, este posibil să se ofere criterii pentru corectitudinea inferențelor, adaptate precis acestei cifre.
Datorită faptului că cifra IV este rar utilizată în practica raționamentului, iar regulile pentru aceasta sunt destul de complicate, nu le vom lua în considerare.
În concluziile primei figuri, premisa mai mică ar trebui să fie afirmativă, iar cea mai mare ar trebui să fie generală.
Un exemplu. Silogismul conform primei figuri:
Toți elevii sunt oameni.
Nici un profesor nu este student.
Nici un profesor nu este o persoană.
este greșită, deoarece premisa mai mică în ea este negativă.
Unii oameni merită respect.
Toți criminali sunt oameni.
Unii criminali merită respect.
Acest silogism pentru prima figură este greșit, deoarece o premisă mare este o propunere privată.
II. O parcelă trebuie să fie negativă, iar cea mai mare - totală.
Toți fizicienii se străduiesc pentru adevăr.
Unii istorici se străduiesc pentru adevăr.
Unii istorici sunt fizicieni.
Această concluzie privind a doua cifră este incorectă, deoarece ambele premise sunt hotărâri afirmative.
Un exemplu. Silogismul conform celei de-a doua figuri:
Unii oameni pot fi tați.
Nici o femeie nu poate fi tată.
Unele femei nu pot fi umane.
este incorectă, deoarece o premisă mare este o judecată privată.
Cel mai mic premis trebuie să fie afirmativ, iar concluzia - privată.
Toți elevii sunt oameni.
Unii studenți nu sunt bărbați.
Unii oameni nu sunt oameni.
Acest silogism al celei de-a treia figuri nu este corect, deoarece premisa mai mică din aceasta este negativă.
Toți elevii sunt oameni.
Toți elevii sunt ființe vii.
Toate ființele vii sunt studenți.
Acest silogism al celei de-a treia cifre este greșit, deoarece concluzia sa este o judecată generală.
Ghidat de regulile generale ale silogismului și ale regulilor figurilor, este ușor să distingem modurile corecte ale silogismului de cele greșite. Desigur, prezentarea unui exemplar contrare este o procedură mai atractivă. Cu toate acestea, aceasta nu are sistematicitate și valabilitate. Regulile vă permit să eliminați în mod sistematic concluzii greșite și să justificați acceptabilitatea concluziilor corecte. Dacă stabilim că silogismul îndeplinește toate regulile, atunci putem fi siguri că este corect. Exercitarea aplicării acestor reguli în silogismele specifice vă va ajuta treptat să vă dezvoltați abilitatea de a distinge concluziile corecte de cele greșite. Aceasta este o cultură logică.