Teoria jocurilor este concepută pentru a rezolva situații de conflict. și anume Situațiile în care interesele a două sau mai multe părți, care urmăresc obiective diferite, se ciocnesc.
Dacă scopurile părților sunt direct opuse, atunci vorbește despre un conflict antagonist.
Jocul este un model simplificat formalizat al unei situații de conflict.
O desenare unică a jocului de la început până la sfârșit se numește petrecere. Rezultatul lotului este o plată (sau o victorie).
Jocul constă în mișcări. și anume alegerea jucătorilor dintr-o serie de alternative posibile.
Mișcările pot fi personale, aleatorii. în contrast cu cel aleator. presupune o alegere conștientă a jucătorului de o variantă.
Jocurile în care există cel puțin o mișcare personală sunt numite strategice.
Jocurile în care toate mișcările sunt aleatoare sunt numite jocuri de noroc.
Atunci când fac o mișcare personală, aceștia discută și despre strategia jucătorului, adică Pe regula sau pe un set de reguli care determină alegerea jucătorului. În acest caz, strategia ar trebui să fie cuprinzătoare, adică Alegerea ar trebui determinată pentru orice situație posibilă în timpul jocului.
Sarcina teoriei jocurilor este de a găsi strategiile optime pentru jucători, adică strategii care le oferă câștiguri maxime sau pierderi minime.
Clasificarea modelelor teoretice de joc
Jocul n persoanelor este de obicei denumit unde, unde
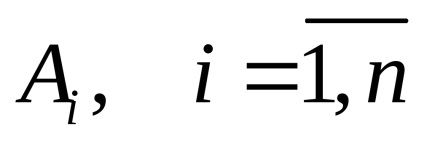
În conformitate cu această desemnare, se poate propune următoarea clasificare a modelelor teoretice de joc:
Discrete (seturi de strategii

Continuă (seturi de strategii

Antagonist (jocuri cu suma zero)
(interesele părților sunt opuse, adică pierderea unui jucător este egală cu câștigurile celuilalt)
Cu informații complete (dacă jucătorul care face o mișcare personală cunoaște întreaga preistorie a jocului, adică toate mișcările adversarului)
Cu informații incomplete
Cu o sumă zero (suma totală este zero)
Cu o sumă nonzero
Reprezentarea matriceală a unui joc antagonic de perechi
În acest manual vom examina jocurile antagonice ale a două persoane. date sub formă de matrice. Acest lucru înseamnă că noi știm o mulțime de strategii primului jucător (jucător Istoria) Ai>, i = 1, ..., m și setul de strategii al doilea jucător (igrokB) Bj>, j = 1.N. și, de asemenea, matricea A = || aij || câștigă primul jucător. Deoarece acesta este un joc antagonic, se presupune că câștigul primului jucător este egal cu pierderea celui de-al doilea jucător. Noi credem că matritsyaij elementul - câștigând primul jucător din selecție îl strategiiAi și să răspundă la el al doilea jucător strategieyBj. Un astfel de joc va fi marcat ca
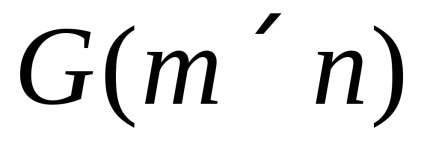
Nu este dificil să vezi că acest joc este antagonic, în plus, este un joc cu informații incomplete, pentru că jucătorul B care face o mișcare personală nu știe ce alegere a făcut jucătorul.
După cum sa menționat mai sus, problema teoriei jocurilor este de a găsi strategiile optime pentru jucători, adică strategii care le oferă câștiguri maxime sau pierderi minime. Acest proces se numește decizia jocului.
Atunci când decideți jocul în formă de matrice, ar trebui să verificați jocul pentru prezența unui punct de șa. Pentru aceasta, sunt introduse două valori:
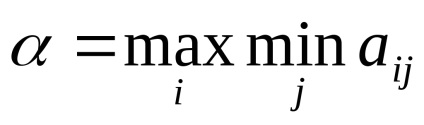
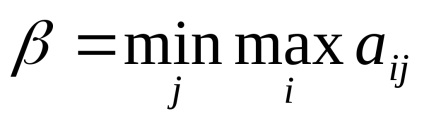
Primul jucător este de natură să aleagă strategia sub care se va obține câștig maxim între toate reacțiile posibile ale al doilea jucător, iar al doilea - dimpotrivă, cea care minimizează pierderea propriei sale, și anume, o posibilă victorie a primului.
Se poate dovedi că α ≤ V≤ β. unde V este prețul jocului. și anume victorie probabilă a primului jucător.
Dacă relația α = β = V este satisfăcută. atunci ei spun că jocul are un punct de șa
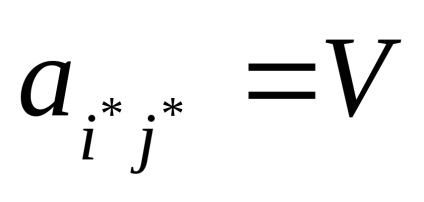
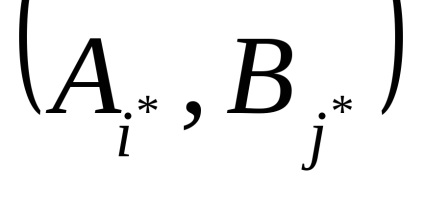
Să revenim la jocul considerat de noi în exemplul 1 și să-l verificăm pentru prezența unui punct de șa.
Acest joc este cu informații complete.
În acest caz
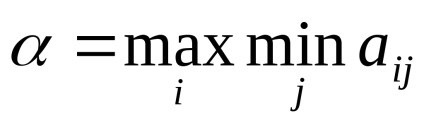
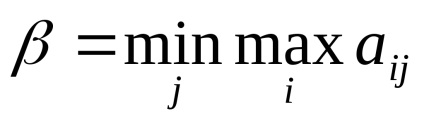
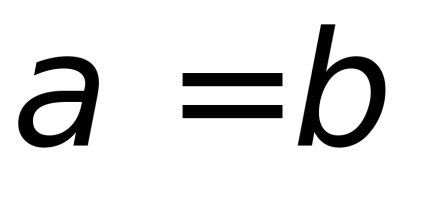
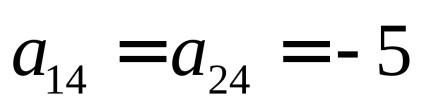
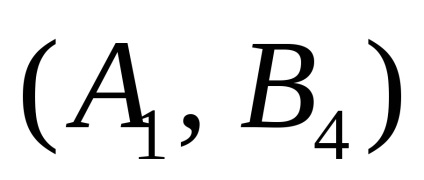
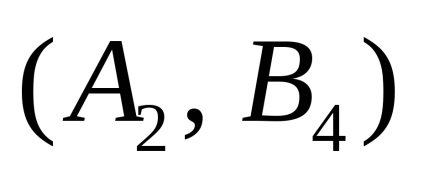
Exemplele 2 și 3 reprezintă o bună ilustrare a teoremei următoare, dovedită în teoria jocurilor:
Orice joc adversar cu informații complete este rezolvat în strategii pure.
astfel Teorema 1 spune că orice joc de două persoane cu informații complete are un punct de șa și există o pereche de strategii pure
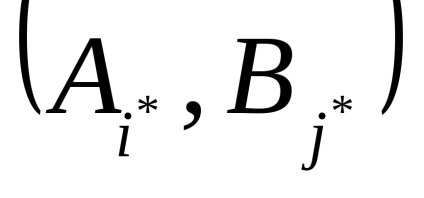
Vsluchae punct aceeași lipsă de șa, sunt folosite ca soluții t.n.smeshannye strategie, gdepiiqj - probabilități de selecție Bj strategiyAi și primul și al doilea jucători, respectiv. Soluția jocului în acest caz este o pereche de strategii mixte
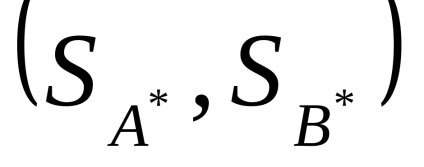
Următoarea teoremă servește ca o generalizare a teoremei 1 în cazul unui joc cu informații incomplete:
Orice joc adversar cu perechi are cel puțin o soluție optimă, adică pereche în cazul general al strategiilor mixte
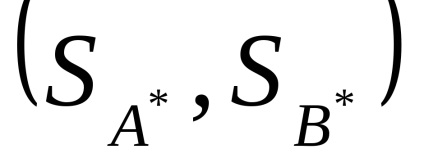
În cazul particular pentru un joc cu un punct de șa, soluția în strategii mixte arată ca o pereche de vectori în care un element este egal cu unul, iar restul este egal cu zero.