Calculul aproximativ al rădăcinilor ecuațiilor
Sarcina: Separați o rădăcină a ecuației și calculați-o pe intervalul rezultat [a; b] până la 0,0001 prin trei metode.
A) metoda de dihotomie
B) metoda simplă de iterație.
D) Metoda acordurilor.
soluţie:
a) rezolva ecuația prin metoda simplă de iterație
Împărțim rădăcina, pentru aceasta transformăm ecuația în forma:
și să construiască grafice de funcții.
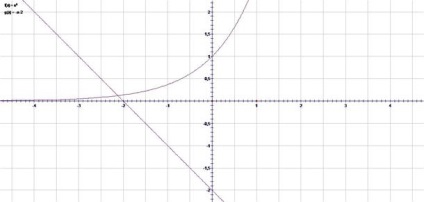
Intersecția acestor grafice este vizibilă în intervalul [-3; -2]; Vom căuta rădăcina în acest interval.
Transformăm ecuația în formă
.
Am ales prima aproximare.
astfel cu precizia necesară
b) rezolva ecuația prin metoda dihotomiei (împărțind segmentul pe care rădăcina este separată, în jumătate).
ecuația:
Segmentul pe care vom căuta rădăcina [-3; -2].
la capetele unui segment, funcția are semne diferite
Considerăm intervalul [-2,5; -2], deoarece la capetele sale funcția ia valori diferite pentru semn.
Luați în considerare segmentul [-2,25; -2], deoarece la capetele sale funcția ia valori diferite pentru semn.
Să considerăm intervalul [-2,125; -2]; la capetele sale funcția ia valori diferite pentru semn.
Să luăm în considerare intervalul [-2,125; -2,0625]; la capetele sale funcția ia valori diferite pentru semn.
Luați în considerare intervalul [-2,125; -2,09375], deoarece la capetele sale funcția ia valori diferite pentru semn.
Luați în considerare intervalul [-2,125; -2,109375], deoarece la capetele sale funcția ia valori diferite pentru semn.
Să luăm în considerare intervalul [-2,125; -2,1171875]; la capetele sale funcția ia valori diferite pentru semn.
Luați în considerare segmentul [-2,12109375; -2,1171875], deoarece la capetele sale funcția ia valori diferite pentru semn.
Să luăm în considerare intervalul [-2,12109375; -2,119140625]; la capetele sale funcția ia valori diferite pentru semn.
pentru că , atunci rădăcina se găsește cu o precizie dată
D) rezolva ecuația prin metoda chordului.
ecuația:
Formula de iterație are forma:
Rădăcina se găsește cu o precizie dată
concluzie:
În rezolvarea acestei ecuații, rădăcinile sunt obținute în trei moduri:
Valoarea funcției Ecuația: la aceste puncte este egală cu
0.00003163
-0.00008037
Ie nu este semnificativ diferit de zero. Diferențele în sensul rădăcinilor din primul, al doilea și al treilea caz sunt explicate prin diferite criterii pentru oprirea procesului iterativ