AGENȚIA FEDERALĂ PENTRU EDUCAȚIA FEDERAȚIEI RUSIEI
UNIVERSITATEA DE RADIOLOGIE DE STAT DE RĂZAZAN
"Sinteza caracteristicilor de frecvență ale sistemelor liniare de comandă automată"
Arta finalizată. c. 511
logaritmic frecvență deschis bucla
1. Construiți caracteristicile de frecvență logaritmică ale sistemului deschis în funcție de indicatorii de calitate specificați.
2. Determinați rezervele de stabilitate LAX și LFH prin consolidare și fază.
3. Notați funcția de transfer a sistemului deschis pe LAX construit.
4. Calculați și construiți răspunsul de frecvență al unui sistem închis.
1. Eroare constantă: în funcție de tulburarea (# 948; st / x0) · 10 2 = 0,5
2. Frecvența tăierii: Cp (2 + n) · 10 -2 = 3, unde n = 1
3. Coeficientul de transmisie logaritmică L01 la frecvența 0,1 # 969, cu un minim de 26 dB.
4. Stabilitatea la fază # 916; # 966; ± 10 0 = 40 0
5. Timp constant al legăturilor inerțiale obligatorii: Tin1 · 10 4 = 7, Tin2 · 10 5 = 3
6. Frecvența interferenței armonice (# 969; n / # 969; cp); 10 -2 = 3
7. Factorul de suprimare a interferențelor Lp nu este mai mic de 80 dB
Construcția LAX și LPC a unui sistem deschis
Construcția lui LAX începe cu o asimptote cu frecvență joasă. pentru că Este stabilită o eroare statică, sistemul va fi static. Panta LAX pentru asimptota cu frecvență joasă va fi zero și eroarea este dată de # 948; c = x0 / (1 + k).
k = x0 / # 948; st -1 = 2 * 10 2 -1 = 199 este coeficientul de transmisie al sistemului deschis
L1 = 20lg (k) = 20lg (199) = 46 este coeficientul de transmisie logaritmică al sistemului deschis
Ie asimptota cu frecvență joasă este purtată prin m (1; 46) paralel cu axa de frecvență.
Pentru a asigura marja necesară de stabilitate a fazei, este necesar ca LAX să traverseze axa de frecvență la o înclinare de -20 dB / dec la frecvența de cutoff.
Secțiunile construite ale LAX sunt conectate printr-o linie dreaptă la o pantă de -40 dB / dec, în timp ce pentru a furniza elementul 3 al datelor originale, selectăm C1 = 5pd / s, apoi t. (10; 26) (t # 969; cp; L01)) va trece sub linia dreaptă cu panta zero.
Conjugarea frecvenței C2 este aleasă din starea de marjă de stabilitate în fază # 916; # 966; ± 10 0 = 40 0 (deoarece legăturile inerțiale tipice și obligatorii ulterioare vor introduce o modificare de fază suplimentară): # 969; c2 = Cp / 2 = 50 rad / s.
Construit LAA format în urma unități de conexiune din seria tipică: freewheeling k (p) = 199, două inerțial k (p) = 1 / (1 + T1 p) și rapel 2 k (p) = (1+ T2 p). astfel funcția de transfer a conexiunii legăturilor tipice va arăta astfel:
LFR a funcției de transfer rezultate este construită prin adăugarea LFH a legăturilor individuale.
Se poate vedea din figură că, atunci când este legată o legătură liniară tipică, LPC-ul sistemului nu se încadrează într-un anumit interval de stabilitate în fază. Pentru a asigura această condiție, o legătură inerțială suplimentară cu o frecvență de interfață C3 situată deasupra frecvenței cutoff. Un sistem cu o legătură inerțială suplimentară va trece într-un interval dat la C3 = 333rad / s.
Dostraivalos LAA și LPC sistem ținând cont de legare unități inerțiale revendicării 5 datele originale și verificați pentru suprimarea unei interferențe armonice 6 și 7 datele inițiale link-ul introdus:
Se poate vedea în figura 1 că (30 · 10 3; -80) se află deasupra bucla deschisă a sistemului deschis, de unde este îndeplinită cerința de suprimare a interferenței armonice.
Determinarea stocurilor de stabilitate
Desenăm grafic construcțiile construite LAX și LPC ale unui sistem deschis.
Stabilitatea armăturii L = 24 dB.
Rezerve de stabilitate a fazelor # 916; # 966; = 45 °.
Înregistrarea funcției de transfer a unui sistem deschis cu privire la un LAX asimptotic
La frecvențe apropiate de 0, LAX are o pantă zero, ceea ce înseamnă că este format din legătura inerțială cu funcția de transfer k (p) = k. Pe C1 pantă se schimbă cu - 40 dB / dec - această pantă este asigurată de 2 legături inerțiale cu k (p) = 1 / (1 + T1 p) 2. T1 = 1 / # 1; Cu o astfel de pantă, LAX merge la # 969; c2. și apoi panta devine egală cu -20 dB / dec. Schimbarea pantei cu + 20 dB / dec este asigurată de legătura forțată cu k (p) = (1 + T2 p), T2 = 1 / # 969; c2. Pe C3, panta se modifică cu -20 dB / dec și devine -40 dB / dec, adică legătura inerțială cu k (p) = 1 / (1 + T3 p). Pe # 969; .. in1 schimbări de pantă la - 20 dB / decadă, și este egală cu - 60 dB / decadă, adică acționează elementul inerțial cu k (p) = 1 / (1 + p Tin1). Pe # 969; .. IN2 schimbări de pantă la - 20 dB / decadă, și este egal cu - 80 dB / decadă, adică acționează elementul inerțial cu k (p) = 1 / (1 + p TUH2).
În construcția unei buclă deschisă LAX s-au folosit legături liniare tipice, astfel încât funcția de transfer a acestui sistem poate fi scrisă ca un set de astfel de legături.
,
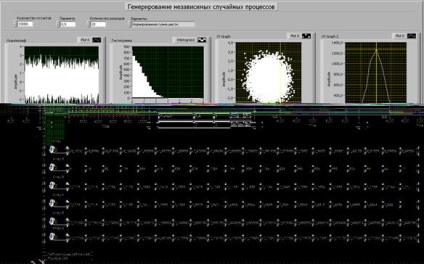
Generarea de procese aleatorii independente
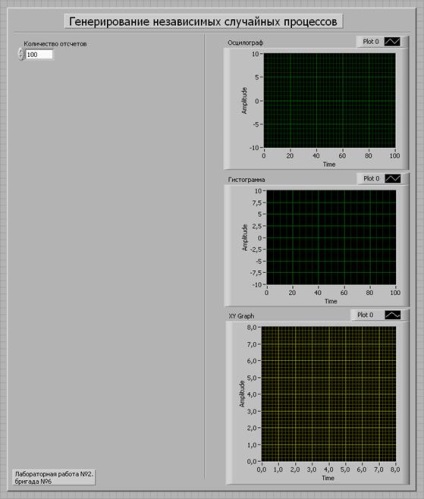
1. Formați panoul frontal în conformitate cu instrucțiunile metodologice de lucru în laborator.
Apoi, în fereastra BlockDiagram, adăugați elementele lipsă: structura ForLoop și creați elementul histogramă. Atunci vom conecta toate elementele în mod corespunzător. Setați numărul de numere la 100 și executați simularea.
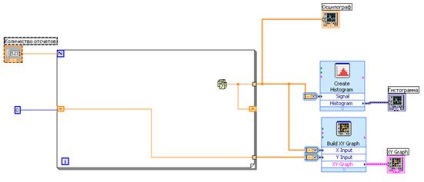
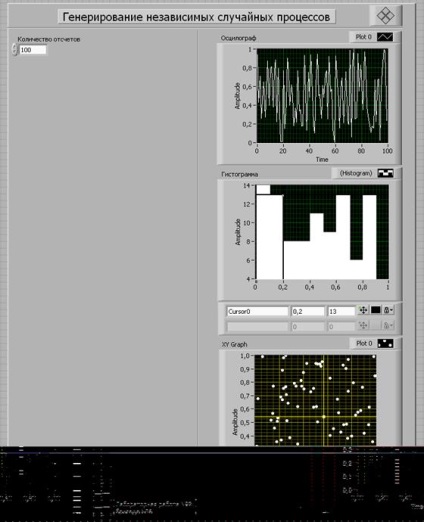
Calculăm eroarea relativă maximă de calcul al probabilității pentru un număr diferit de probe N:
dmax = | 10 -15 | / 10 = 0,5
dmax = | 100 -124 | / 100 = 0,24
dmax = | 1000 -945 | / 1000 = 0,065
dmax = | 10000 -10129 | / 10000 = 0,0129
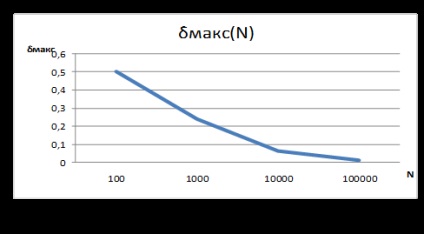
Se crede că N (numărul de experimente) și m (numărul de cifre) ar trebui găsite în următoarea relație:
Această relație se explică prin faptul că, atunci când numărul de cifre crește, este necesar să se mărească numărul de numere. Altfel, histograma distribuției va fi robustă și nu ne va permite să judecăm distribuția unei variabile aleatorii cu o precizie bună.
2. Generarea unei secvențe aleatorii cu o lege de distribuție care este diferită de cea uniformă prin metoda funcției inverse.
Structura ForLoop a fost copiată - un generator al unei secvențe aleatoare uniform distribuite. În comutatorul de opțiuni este setată "Transformarea neliniară". În câmpul gol rezultat, a fost inserată o structură ForLoop copiată. În interiorul structurii ForLoop, o diagramă bloc a programului este generată folosind formula u = s (-2ln (1 - x)) 1/2.
Setați valoarea parametrului în conformitate cu versiunea - 0.5 și numărul de numere - 1000.
Am început simularea. Noi compunem tabelul dependenței ni (x), pi (x),:
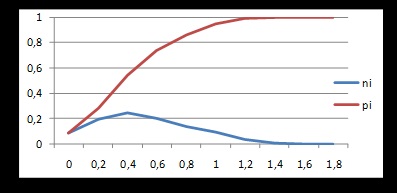
3. Generarea de secvențe aleatoare prin adăugarea unor secvențe aleatoare uniform distribuite (numărul variabilelor aleatorii pliabile este de la 2 la 6).
Să adăugăm încă 6 variante: "Suma celor două uniforme", "Suma celor trei uniforme", "Suma celor patru uniforme", "Suma celor cinci uniforme", "Suma celor șase uniforme", "Suma normalizată a șase uniforme".
Pentru fiecare variantă, colectăm schemele corespunzătoare din structura Casei.
1) suma a două uniforme:
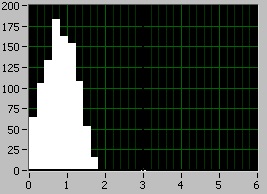
2) Suma a trei uniforme
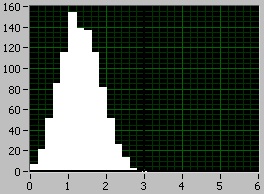
3) Suma a patru uniforme
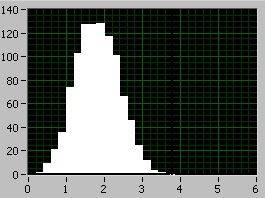
Rezultatele obținute sunt explicate prin faptul că se adaugă primul și al doilea moment al variabilelor aleatoare. Ie cu creșterea cantității pentru un termen de așteptare mat este crescut cu 0,5 (valoarea saltelei. standby pentru intervalul uniform variabilă aleatoare 0-1) și despersiya asemenea incrementat cu 1 (valoarea dispersiei la interval de uniformă valoare aleatoare 0-1).
4. Determinarea proximității legii distribuției a sumei normalizate a șase variabile aleatorii distribuite uniform la legea normală.
În ferestrele BlockDiagram și FrontPanel vom adăuga noi elemente necesare pentru rezolvarea problemei: