În primul rând, trebuie să puteți să compuneți SDNF și SKNF, deoarece este posibil să fie și în control. Ce este posibil să citești și în materiale și în alte surse accesibile. Pe scurt, SKNF este o formă normală perfect conjugată, iar SDNF este o formă normală complet disjunctivă.
Destul de conjunctivă NP - o conjuncție disjuncțiilor, și în fiecare disjuncție (în fiecare suport) conține toate variabilele din formula sau negația ei nu este același disjunctiile, fiecare disjuncție este termeni nu identici:
Absolut disjunctiv NF - disjuncția conjuncțiilor. și în fiecare conjuncție există toate variabilele care intră în formula, sau negarea lor, nu există conjuncții identice, în fiecare conjuncție nu există termeni identici:
Acum, ia în considerare un exemplu în care, folosind tabelul de adevăr, construim SDNF și SKNF și apoi continuăm să minimalizăm.
De exemplu, luați o funcție cu trei variabile și ați analizat deja în lecție.
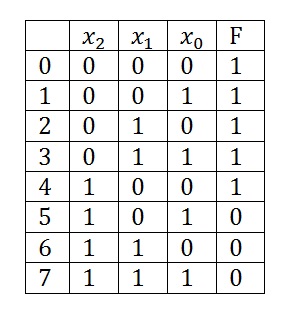
Luați în considerare punctele privind modul de compilare a CDNF:
1. Scriem produsul seturilor de variabile. dacă funcția este 1 (F = 1);
2. Luăm o variabilă cu o valoare negativă dacă valoarea ei este 0
3. Între fiecare produs dintr-un set de variabile, punem semnul adăugării logice
Acum, să compilați CDNF pentru tabelul nostru de adevăr.
Luați în considerare punctele privind modul de compilare a SKNF:
1. Scriem produsul seturilor de variabile. dacă funcția este 0 (F = 0);
2. Luați o variabilă cu o valoare negativă dacă valoarea ei este 1;
3. Între fiecare produs dintr-un set de variabile, punem semnul adăugării logice
Noi compunem SKNF pentru tabelul de adevăr.
Acum, să trecem la minimizarea funcțiilor.
În primul rând, să ne uităm la modul în care vom simplifica SDNF și SKNF. Să începem cu SDNF:
Acum căutăm perechi de termeni care diferă doar într-o singură variabilă, adică într-un caz este negativ, în celălalt caz fără. Selectăm astfel de perechi (în cazul în care perechile vor avea aceleași culori):
Dar este important de remarcat că, dacă împărțiți cuvintele în perechi, atunci una dintre silabe va rămâne fără pereche. Și aici ne îndreptăm spre axiomele algebrului logicii: Continuând de aici, facem următoarele transformări:
Acum, împărțiți sloganul în perechi și să ia parantezele de aceeași variabilă, atunci conținutul paranteze sunt reduse (cum și de ce se întâmplă acest lucru, trebuie să știți):
Acum, hai să mergem la minimizarea SKNF. Principiul este identic cu cel al SDNF:
Cel mai probabil vom avea controlul asupra SDNF, dar trebuie să fim pregătiți și pentru SKNF. Și acum ce anume va fi în camera de control. Carnota Carnot este un alt mod de a minimiza.
Vom lucra deja cu masa de adevăr pe care o avem. În primul rând, tragem următorul tabel:
Trebuie notat separat numerotarea din tabel. Ar trebui să-ți amintești de asta.
Acum umplem masa. Celulele corespunzătoare se umple cu 1 dacă F = 1 și se lasă goale sau se stabilește la 0 dacă F = 0:
Acum, căutați grupuri de 1 vecini care sunt în buclă. În apropiere sunt 1, stând una lângă alta orizontal și vertical. Deci, sunt adiacente extreme 1, adică 1 din celule prezintă 0 celule vecine 1 din 2. Dacă este dificil să înțelegem ce înseamnă să „locuiască“, vă puteți aminti că unitățile grupului poate consta din 2, 4, 8, precum și orice alt Online unități la puterea lui n. Și astfel de grupuri se pot lipi doar într-un pătrat sau într-un dreptunghi. De asemenea, în diferite grupuri, dacă este necesar, se poate obține una și aceeași 1. În cele din urmă, am câteva cazuri specifice ia în considerare, dar acum să ne întoarcem la exemplul. Deci, selectați grupurile:
Fie grupul selectat prin negru grupul 1, iar grupul selectat în roșu este grupul 2. Privim grupurile de variabile care rămân neschimbate. În grupul 1, acesta este x2, iar în grupul doi, x1 și x0. Acum ne uităm, ce valori la aceste variabile: dacă 0, luăm o variabilă cu negare, dacă 1, apoi fără. Și obținem următoarea ecuație:
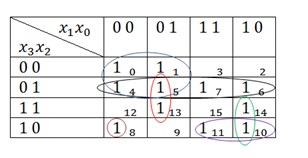
Acum, mai mult despre hărțile lui Carnot. Vom avea funcții cu trei și patru variabile în control, deci aici este tabelul pentru cele patru variabile, trebuie amintit, în special numerotarea.
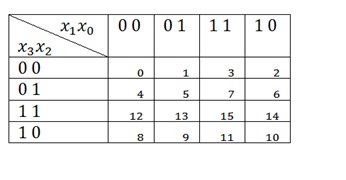
Și acum, pe un astfel de tabel, vom lua în considerare încă două cazuri legate de grupuri de 1:
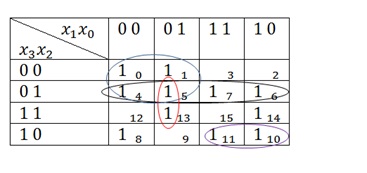
Aici aproape toate 1 sunt atribuite grupurilor. Celulele rămase doar 1 din 14 și 8. În primul rând, o privire la 1 în celula 14. Este adiacent una dintre celulele 6 și 10. Dar, așa cum usche știm că nu poți face un grup de trei 1. În consecință, este posibil să se unească 1 în grupul 1 fie din celula 6, fie din celula 10. Și asta, și asta va fi adevărat. Dar nu puteți combina 1 și 1 din celula 6 și din celula 10. Aceasta înseamnă fie:
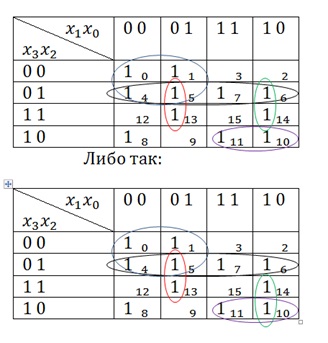
A rămas 1 în cușcă 8. Este simplu. Dacă nu există nimeni cu cine să remedieze, atunci se rezolvă pe sine. Acesta va arata astfel:
Ei bine, cum ar fi, totul. Vor fi întrebări, vă rugăm să contactați. Mult noroc tuturor pentru control!