5. Minimizarea funcțiilor booleene
O funcție implicită este o anumită funcție logică care dispare pe același set de variabile pe care funcția însăși este zero.
Orice termen conjunctivă (conjuncție elementară) sau un grup de termeni, caracterele disjuncție conectate incluse în PDNF sunt implicants funcționale originale
Conjuncția elementară (termen conjunctural), în care unul sau mai mulți termeni primari este îndepărtat, este numit implicit simplu.
Există destul de multe metode de minimizare a funcțiilor Boolean în prezent. Toate acestea, de regulă, constau în două etape. Primul pas este obținerea unei liste a tuturor implicanților simpli, adică abreviat DNP. În cea de-a doua etapă, folosind tabelul de acoperiri, eliminați implicații "extra" de la ceilalți implicați. Drept rezultat, DNF este obținut din care nu pot fi eliminați implicați. Un astfel de DNF este numit un impas.
5.1 Metoda Quine
La prima etapă în metoda perechi Quine compara toate implicants incluse în PDNF, în scopul de a identifica posibilitatea de absorbție a unor variabile pe baza legii de lipire:
.
Procedura continuă până când nu rămâne niciun membru care permite absorbția cu alt termen. Ca urmare, se obțin un număr de implicați simpli. Disjuncția acestor implicați este un DNP abreviat.
În cea de-a doua etapă, se construiește un tabel de acoperire. Rândurile din acest tabel indică implicații simpli găsiți, iar în coloane - termenii expresiei funcției inițiale. Celulele de masă sunt marcate dacă un implicant simplu este inclus într-un termen. Ca urmare, minimizarea unei funcții booleene reduce la găsirea unui număr minim de implicați simpli care acoperă toate coloanele. Ca rezultat, se obține un DNF cu capăt închis.
Dezavantajul metodei este nevoia de comparare pe perechi a tuturor termenilor conjunctivi în prima etapă atunci când se găsesc implicați simpli. Cu un număr din ce în ce mai mare de termeni inițiali, numărul de comparații pe perechi crește, ceea ce complică rezolvarea problemei de minimizare.
5.2 Metoda Quine folosind cuburi n-dimensionale
Această metodă elimină dezavantajul metodei anterioare, adică elimină necesitatea unei comparații pe perechi a tuturor termenilor în prima etapă atunci când se găsesc implicați simpli. Pentru a face acest lucru, vom construi cubul n-dimensionale pe care le poate identifica vizual legătura pe termen conjunctivă care generează implicants simple.
Atunci când rezolvăm problema minimizării unei funcții booleene, este convenabil, în loc de termeni conjunctiv, să folosim seturi binare corespunzătoare acestora.
Minimizați funcția Boolean
.
Aici în paranteze sunt echivalentele zecimale ale seturilor binare corespunzătoare.
Reprezentăm funcția sub forma unui CDNF:
Scriem termenii conjunctivi sub forma de seturi binare:
.
Unitatea 4 constructul - cub dimensionale și selectați nodurile seturilor binare incluse în funcția Boolean specificată corespunzătoare (Figura 10.):
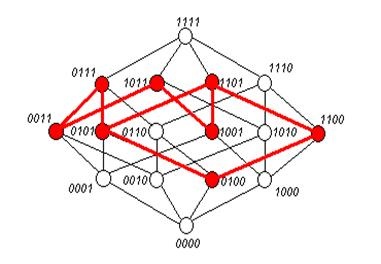
1 etapă. Definiția abreviated DNP.
Aplicăm legea de lipire pentru vârfurile marcate (pentru seturile binare) ale unui cub conectat printr-o margine:
O linie indică faptul că în acest moment nu există nicio variabilă.
Pentru unii implicați simpli, lipirea poate fi continuată:
Prin legea idempotenței:
Disjuncția implicării simple rezultate este un DNP abreviat:
2 etape. Definiția dead end DNF.
Pentru a determina DNF-ul mort, vom construi un tabel de acoperitoare, care ar trebui să includă seturi binare care nu au participat la lipire:
Determinând numărul minim de rânduri care acoperă toate coloanele tabelului, găsim blocajul DNF:
Dezavantajul metodei este construcția unui cub n-dimensional, deoarece pentru o serie de variabile această construcție este dificilă.
5.3 Metoda Quine-McCluskey
Metoda Quine-McCluskey este metoda anterioară, dar fără construcția geometrică a cuburilor n-dimensionale: cuburile sunt prezente, dar abstracte.
Metoda se bazează pe o reprezentare cubică a termenilor conjunctivi ai DNF cu o subdiviziune preliminară a cuburilor în subgrupuri determinate de același număr. Partiționarea face posibilă compararea cuburilor grupurilor care sunt învecinate cu numărul de unități pentru a reduce numărul de căutări.
În cadrul procedurii de minimalizare iterativă, o comparație pe perechi poate fi făcută numai între grupurile învecinate.
Găsirea unei implicări simple în prima etapă:
1. Toți termenii conjunctivi inițiale sunt scrise sub forma seturilor lor binare.
2. Toate seturile sunt împărțite în grupuri disjuncte după numărul de grupuri. Formarea Condiții de r-cub - prezența diferențelor în (r-1) -cube numai o coordonată într-o formă binară și având coordonatele independente comune.
3. Grupul i include toate seturile binare care au unități în înregistrarea lor.
4. Comparația între perechi se face numai între grupurile adiacente prin număr. Grupuri care diferă în două cifre sau mai mult, nu are sens să se compare.
Minimizați funcția Boolean
Informații despre lucrarea "Logică matematică"
Sectiunea: Matematica
Numărul de caractere cu spații: 29947
Număr de mese: 14
Număr de imagini: 9
afirmă sau neagă orice legătură între obiecte și fenomene ale realității. 3. Logica mathematică și "bunul simț" în secolul XXI. Logica nu este doar matematică, ci și o știință filosofică. În secolul al XX-lea, aceste două ipostaze interconectate ale logicii s-au dovedit a fi divorțate în direcții diferite. Pe de o parte, logica este înțeleasă ca știința legilor gândirii corecte.
divertisment. Exercițiile sunt de același tip. Prin urmare, este pur și simplu necesar să se completeze datele din exercițiul de exerciții cu sarcini suplimentare de natură în curs de dezvoltare. Capitolul II. Metoda de studiere a elementelor de algebră și logică matematică. § 1. Metoda de studiere a expresiilor numerice, expresii cu variabile, egalități numerice și inegalități, ecuații. Studiul expresiilor numerice, egalității și inegalităților, a.
declarația "Nu folosesc niciodată metodele logicii matematice." Evident, ele se contrazic reciproc, dar ar putea fi simultan false. De exemplu, dacă sunteți un specialist în logica matematică, atunci ar trebui să utilizați adesea metodele sale, dar cu greu aveți nevoie de ele în fiecare zi din viața voastră. Legea mijlocului exclusiv este destinată utilizării în domeniul științelor exacte.
postulate D (adică axiome Ax # 204; F # 205; A * și deductiv înseamnă P # 204; Fn + 1), atunci vorbim despre construirea unei teorii ca sistem formal al F.S. =