coeficientul de dilatare liniară a solidelor.
Obiectiv: determinarea coeficientului de temperatură pentru dilatarea liniară a barelor din materiale dure.
Echipamente: dispozitiv pentru determinarea coeficientului de dilatare liniară (PRTT), probe de tije (oțel, aluminiu, sticlă), indicator IC, etrier.
Când temperatura se schimbă, volumul solidului se schimbă: pe măsură ce crește temperatura, volumul crește, iar când corpul se răcește, se contractă. Fenomenul schimbării mărimii și volumului de solide cu o schimbare de temperatură se numește expansiune termică.
Care sunt motivele pentru expansiunea corpurilor când sunt încălzite? De ce, atunci când sunt încălzite (răcite), distanțele medii dintre atomi cresc (scăderea)?
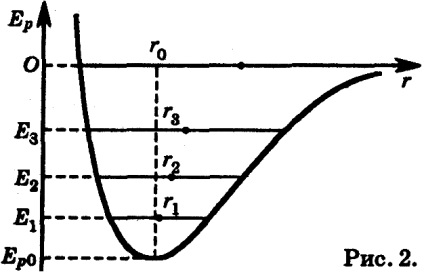
Imaginea moleculară a expansiunii termice. Dependența energiei potențiale a interacțiunii moleculelor cu distanța dintre ele face posibilă determinarea cauzei apariției expansiunii termice. Luați în considerare în Fig. 1 și Fig. 2 cum depind forțele interacțiunii intermoleculare a moleculelor și energia potențială a interacțiunii moleculelor cu distanța dintre ele.
E
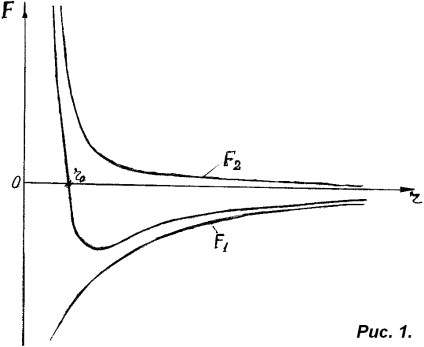
Astfel, molecula (atomul) se află în interiorul puțului potențial și face oscilații fără să părăsească această "groapă", de la un "perete" la celălalt.
Curba potențială de energie este puternic asimetrică. Ea crește foarte rapid de la valoarea minimă a Ep0 cu scăderea lui r și crește relativ încet cu creșterea r. La zero absolută într-o stare de echilibru, moleculele ar fi la o distanță r0 una de cealaltă. care corespunde valorii minime a energiei potențiale Ep0. Pe măsură ce crește încălzirea, energia cinetică a moleculelor crește și încep să oscileze în apropierea poziției de echilibru. Gama de oscilații este determinată de valoarea medie a energiei. Dacă curba potențială a energiei a fost simetrică, atunci poziția medie a moleculei ar corespunde în continuare distanței r0. Ce ar însemna invarianța generală a distanțelor medii între molecule după încălzire, armonicitatea oscilațiilor în jurul poziției de echilibru și, în consecință, absența expansiunii termice.
De fapt, atomii din grila de cristal efectuează oscilații anharmonice (adică, non-armonice).
Pe măsură ce crește temperatura, oscilațiile oscilațiilor cresc; energia (nivelul de energie) al particulelor crește. Astfel, de exemplu, la o temperatură T1, nivelul de energie este E1. la T2 - nivelul E2. În primul caz, particula oscilează în apropierea poziției r1. în al doilea cu o amplitudine mai mare - aproximativ r2. care corespund noilor poziții de echilibru. Se poate observa din figura 2 că, odată cu creșterea temperaturii, acest punct - punctul poziției de echilibru - se îndreaptă spre dreapta, adică în direcția distanțelor interatomice mari. Prin urmare, cauza expansiunii termice a corpurilor este evidentă.
K
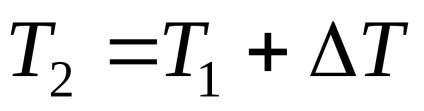
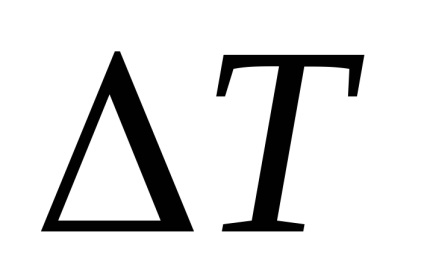
și anume semnificația fizică a coeficientului de dilatare liniară α - coeficientul de expansiune liniară α indică la ce proporție din valoarea sa inițială dimensiunile liniare ale corpului se schimbă cu o schimbare de temperatură cu un Kelvin.
În mod similar, coeficientul de expansiune volumetrică β este determinat din relația:
și anume coeficientul de expansiune a volumului β este egal cu schimbarea relativă a volumului
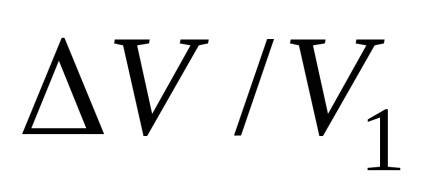
Din (1) și (2) rezultă că
Din cauza anizotropiei cristalelor, coeficientul de expansiune liniară

Pentru cristalele cu simetrie cubică, precum și pentru corpurile izotropice (majoritatea metalelor), coeficientul de dilatare liniară este același în toate direcțiile, iar în acest caz
Coeficienții de dilatare liniară rămân practic constanți dacă intervalele de temperatură în care sunt măsurate sunt relativ mici (câteva zeci de grade). În general, coeficienții de expansiune termică (




Pentru cele mai multe substanțe, coeficientul de dilatare liniară este mic, iar valorile sale sunt 10 -5 ÷ 10 -6 K -1. În mod deosebit mic este coeficientul de dilatare liniară în intervalul de temperaturi de la -30 ° C la +100 ° C în Invar (un aliaj de fier și nichel). Prin urmare, Invar este utilizat pentru a produce instrumentele exacte folosite pentru determinarea dimensiunilor corpurilor. Dimensiunile liniare ale instrumentului însuși din Invar depind foarte puțin de fluctuațiile de temperatură.
Expansiunea termică a corpurilor este luată în considerare la proiectarea tuturor instalațiilor, instrumentelor și mașinilor care funcționează în condiții de temperatură variabilă.
în
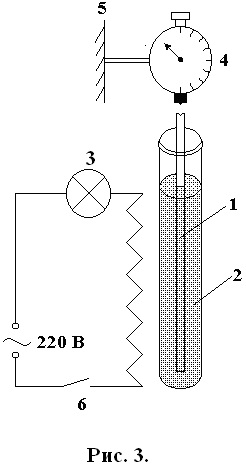
Încălzitorul este conectat la rețeaua de 220 V cu ajutorul butonului (6); atunci când porniți, lumina (3) trebuie să se aprindă. Tijele de testare sunt încălzite de la temperatura camerei până la punctul de fierbere al apei de 100 ° C (373 K).
Ordinea de executare a muncii
Sarcina 1. Măsurarea alungirii tijelor în timpul încălzirii și calcularea coeficientului de dilatare liniară.
Măsurați lungimea inițială a tijei ℓ1 și temperatura corespunzătoare T1 (temperatura camerei) cu o etrier.
Introduceți tija (1) în tubul de testare (2) și umpleți-o cu apă la un centimetru sub marginea tubului (2).
Introduceți tubul cu tija în priza încălzitorului, aduceți tija indicator (4) și montați-o pe tija. În timp ce țineți carcasa indicatorului cu mâna și rotiți colivia, setați punctul zero al scării până la capătul săgeții.
Porniți încălzitorul (6). Dacă are loc o evaporare intensă, opriți încălzitorul cu butonul (6) și supravegheați (încălzirea inerțială va continua) după indicarea indicatorului. Indicația maximă a indicatorului, care corespunde fierberii apei, este

Cu atenție (cu o cârpă uscată), scoateți tubul cu tija de la încălzitor, turnați apa caldă și plasați tubul în tubul de testare.
Acțiunile și măsurătorile similare (vezi punctele 1-5) fac cu alte tije.
După răcirea tijei și a tubului la temperatura camerei, repetați măsurarea.
Calculați coeficientul mediu de temperatură
