12. Teorema privind suma unghiurilor unui triunghi (formulare și exemplu).
1. În triunghi, unul dintre unghiuri este 29 °, celălalt 91 °. Găsiți cel de-al treilea colț.
Soluția. Al treilea unghi al triunghiului este
180 ° - (29 ° + 91 °) = 180 ° - 120 ° = 60 °.
2. Găsiți unghiurile ascuțite ale triunghiului drept al isoscelului.
Soluția. Din teorema privind suma unghiurilor unui triunghi rezultă că suma unghiurilor acute ale unui triunghi cu unghi drept este de 180 ° - 90 ° = 90 °. Deoarece unghiurile ascuțite într-un triunghi isoscel dreptunghi sunt egale, fiecare dintre ele este egal cu 90 °. 2 = 45 °.
3. Găsiți unghiurile unui triunghi echilateral.
Soluția. Din teorema privind suma unghiurilor unui triunghi rezultă că suma unghiurilor unui triunghi echilateral este de 180 °. Deoarece toate unghiurile sunt egale într-un triunghi echilateral, fiecare dintre ele este de 180 °. 3 = 60 °.
13. Soluția triunghiului pe trei laturi.
Rezolva triunghiul pe trei laturi - aceasta înseamnă a găsi unghiurile sale pe cele trei laturi date ale triunghiului.

Unicitatea soluției problemei rezultă din egalitatea triunghiului:
Dacă trei laturi ale unui triunghi sunt egale cu cele trei laturi ale unui alt triunghi, atunci aceste triunghiuri sunt egale.
14. Problema pe tema "Linia medie a trapezoidelor".

15. Determinarea sinusului a unghiului ascuțit al unui triunghi cu unghi drept. Un exemplu de aplicație pentru rezolvarea triunghiurilor dreptunghiulare.
Sinusul unghiului ascuțit al unui triunghi drept este raportul piciorului opus cu ipoteza:
1. Având un triunghi drept. Găsiți: a) hypotenuse c și catet L, dacă dăm un catehet a și un unghi opus acestuia;
b) picioarele triunghiului a și b dacă se dau hypotenuse c și unul din unghiurile acute a (Figura 12).
2. În partea de sus a muntelui există o telecabină de 1,2 km lungime, care face un unghi de 60 ° cu înălțimea muntelui. Care este înălțimea muntelui?
Soluția. Indicați lungimea căii prin c, înălțimea muntelui prin A și unghiul dintre telecabină și înălțimea muntelui prin (3) (Figura 13).
Dată: c = 1,2 km, p = 60 °.
Soluția. Din teorema privind suma unghiurilor unui triunghi rezultă că suma unghiurilor acute ale unui triunghi cu unghi drept este de 90 °. Prin urmare, a = 30 °. De aici
16. Proprietatea unghiurilor unui triunghi isoscel.
Un triunghi este declarat a fi isoscele dacă are două părți egale. Aceste părți egale sunt numite laturi, iar a treia parte este numită baza triunghiului.
[P] Într-un triunghi isoscel, unghiurile de la bază sunt egale.
Având: ABC - triunghi izoscel, AB - bază (Figura 14).
Dovedește: unghiul A = unghiul B.
Dovada. CAB triunghi este egal cu CBA triunghi prin primul semn de egalitate

17. Problema pe tema "Similaritatea triunghiurilor".

18. Sarcina pe tema "Parallelogram".
Triunghiul isoscel este inscripționată paralelogram, astfel încât unghiul de paralelogramului coincide cu un unghi la vârf al triunghiului și unghiul la vârf opus situată pe teren. Dovedește că perimetrul paralelogramului este o valoare constantă pentru un anumit triunghi.

19. Determinarea cosinusului unghiului ascuțit al unui triunghi drept. Un exemplu de aplicație pentru rezolvarea triunghiurilor dreptunghiulare.
Cosinul unghiului ascuțit al unui triunghi drept este raportul dintre piciorul adiacent și cel al ipotezei:
1. Având un triunghi drept. Caută:
a) hipotensiunea c și cateterul a dacă sunt date cathetul b și unghiul adiacent acestuia;
b) picioarele triunghiului a și b, dacă li se dă o hypotenuse c și unul dintre unghiurile acute a (Figura 16).

2. Unghiul dintre scara scărilor rulante și podeaua holului este de 150 °. Care este lungimea scării scărilor rulante, dacă talpa scărilor este de 117 m?

20. Un semn al unui triunghi isoscel.
Un triunghi este declarat a fi isoscele dacă are două părți egale. Aceste părți egale sunt numite laturi, iar a treia parte este numită baza triunghiului.
[P] Dacă două unghiuri sunt egale într-un triunghi, atunci este isoscele.

Dovada. Întrucât în triunghi cele două unghiuri sunt egale, laturile care se află sub aceste unghiuri sunt de asemenea egale. Într-adevăr, dacă presupunem că una dintre aceste părți mai mult decât celălalt, atunci unghiul opus, este mai mare decât unghiul, situată împotriva celeilalte părți, iar aceasta contrazice ipoteza (faptul că aceste unghiuri sunt egale). Deci, în triunghiul cele două părți sunt egale, adică triunghiul este isoscele.
21. Problema pe tema "Similaritatea triunghiurilor".
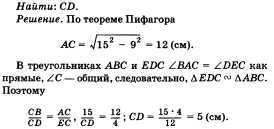
22. Problema pe tema "Dreptunghi".
Partea laterală a dreptunghiului este egală cu 5 cm și 4 cm. Bisectoarele din colțurile adiacente lateralei mari împart partea opusă în trei părți. Găsiți lungimile acestor părți.

23. Determinarea tangentei unghiului ascuțit al unui triunghi drept. Un exemplu de aplicație pentru rezolvarea triunghiurilor dreptunghiulare.
Tangenta unui unghi ascuțit al unui triunghi drept este raportul opus
un picior la adiacente:
1. Având un triunghi drept. Caută:
a) hypotenuse c și catet L, dacă dăm un catehet a și unghiul opus acestuia;
b) și un picior ipotenuză și, în cazul dat cateta s și adiacent la acesta un unghi a (fig. 20).

2. La ce unghi cade fasciculul sol a soarelui, în cazul în care pol vertical blocat în sol se ridică deasupra solului, la 18 m și aruncă o umbră egală cu 73 6 (Fig. 21)?
Indicați lungimea polului cu un a, lungimea umbrei polului prin b și unghiul la care raza soarelui intră pe pământ printr-o a.
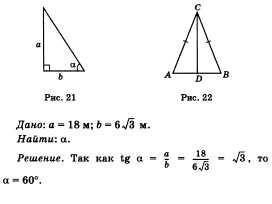
24. Proprietatea mediană a unui triunghi isoscel.
Într-un triunghi isoscel, medianul tras la bază este o bisectrică și o înălțime.
Dată: ABC - triunghi izoscel, AB - bază, CD - mediană (Figura 22).
Dovedește: CD - bisector și înălțime.
Dovada. Triunghiuri CAD și CBD sunt egale, dar a doua caracteristică a egalității de triunghiuri (laturile AC și BC sunt egale, ca ABC - .. Isosceles unghiuri CAD și CBD sunt unghiurile de la baza unui laturi triunghi isoscel AD și BD sunt egale, deoarece D - mijloc segmentul AB).
Egalitatea triunghiurilor CBD și CAD implică egalitatea unghiurilor:
Deoarece unghiurile ACD și BCD sunt egale, CD-ul este un bisector. Deoarece unghiurile ADC și BDC sunt adiacente și egale unul cu altul, ele sunt drepte. În consecință, segmentul CD este și înălțimea triunghiului ABC. Teorema este dovedită.
Astfel, se stabilește că bisectrica, mediana și înălțimea triunghiului isoscel, trase la bază, coincid. Prin urmare, următoarele afirmații sunt, de asemenea, valabile:
1. Bisectorul unui triunghi isoscel tras la baza este o mediană și o bisectrică.
2. Înălțimea unui triunghi isoscel tras la bază este o mediană și o bisectrică.
25. Problema pe tema "Similaritatea triunghiurilor".
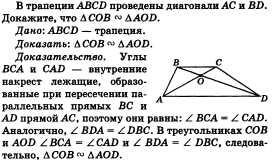
26. Sarcina subiectului "Diamond. Pătrat ".
Dovedeste ca un cerc poate fi inscris intr-un romb.
Dată: ABCD - romb, O - punctul de intersecție al diamantelor rombului.
Dovedeste: O este centrul cercului inscris.
Dovada. Triunghiurile ABO, ADO, CBO și CDO - dreptunghiular (din ABCD - diamant) și sunt de-a lungul ipotenuzei și un picior. În consecință, înălțimile OF și OE extrase din vârfurile unghiurilor drepte sunt egale. Deci, înălțimile de bază se află pe un cerc cu centrul O. Deoarece înălțimea extrasă din nodurile unghiuri drepte, perpendiculare pe laturile rombul, cercul cu centrul O - punctul de intersecție al diagonalelor unui romb - și o rază egală cu distanța de la punctul O la laturile rombul, între părți romburi. Prin urmare, un cerc poate fi înscris în romb.
27. Teorema cosinusului. Un exemplu de aplicație pentru rezolvarea triunghiurilor.
Pătratul oricare latură a triunghiului este egal cu suma pătratelor picioarelor celelalte două laturi fără dublul produs al acestor părți prin cosinusul unghiului dintre ele.

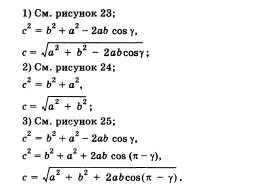

28. Un cerc înscris într-un triunghi.
Se spune că un cerc este înscris într-un triunghi dacă atinge toate laturile sale.
[Π] Teorema în centrul unui cerc înscris într-un triunghi.
Centrul unui cerc înscris într-un triunghi este punctul de intersecție al bisectricei sale.
Având în vedere: ABC este un triunghi dat; O este centrul cercului înscris în el; D, E și F sunt punctele de tangență ale cercului cu laturile triunghiului (Figura 27).
Dovedește: O este punctul de intersecție a bisectorilor.
Dovada. Triunghiurile dreptunghiulare AOD și DOE sunt egale în ipotenuse și un picior. Ei au o hypotenuse OA - obișnuită, iar picioarele OD și OE sunt egale ca raze. Egalitatea triunghiurilor implică egalitatea unghiurilor OAD și OAE. Acest lucru înseamnă că punctul O se află pe bisectoarea triunghiului extras din punctul A. În același mod putem dovedi că punctul O se intinde pe doua Bisectors ale unui triunghi.
[A] Teoremă pe un cerc înscris într-un triunghi.
Un cerc poate fi înscris în orice triunghi.
Având în vedere: A ABC - triunghiul, On - punctul de intersecție al Bisectors, M, L și R - punctul de tangență cu circumferința laturile unui triunghi (Fig. 28).
Dovedește: O este centrul cercului înscris în ABC.
Dovada. Desenați perpendiculele OK, OL și OM de la punctul O în laturile AB, BC și CA (a se vedea figura 28). Deoarece punctul O este echidistant față de laturile triunghiului ABC, atunci OK = OL = OM. Prin urmare, un cerc cu un centru O rază de OK trece prin punctul K L M. Laturile triunghiului ABC ating cercul în punctele K, L, M, deoarece acestea sunt perpendiculare pe razele OK, OL și OM. Prin urmare, un cerc cu centrul O de rază OK este înscris în triunghiul ABC. Teorema este dovedită.
Notă. Rețineți că în triunghi poate fi înscris un singur cerc. De fapt, presupuneți că două cercuri pot fi înscrise într-un triunghi. Apoi centrul fiecărui cerc echidistant față de laturile triunghiului și, astfel, coincide cu punctul O de intersecție a Bisectoarele triunghiului, și o rază egală cu distanța de la punctul O la laturile triunghiului. În consecință, aceste cercuri coincid.
29. Sarcina "liniilor drepte paralele".

30. Problema pe tema "Teorema lui Pitagora".
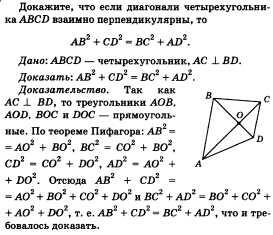
Dovedeste ca daca diagonalele ABCD-ului patrulater sunt reciproc perpendiculare, atunci
Arta similara:
Organizarea unei repetiții generalizate în clasele de geometrie în gradul 7
Curs de lucru >> Pedagogie
Studiul temei Triunghiuri în cursul de geometrie a clasei 7-9 de liceu
Curs de lucru >> Pedagogie
. Pe „Triunghiurile“ pentru clasele 7-9 la revendicarea 1 rezumă lecțiile pe tema „Semne ale egalității de triunghiuri“ (un manual Pogorelov AV Geometrie rezultatele activității lor sunt încurajate cele mai bune răspunsuri orientări: .. Numărul de probe înregistrate.
Răspunsuri la întrebările examenului privind istoria clasei Rusiei 11. Pentru ușurința utilizării, întrebările și răspunsurile sunt postate în ordine cronologică. NI Lobachevski a stat la sursele de geometrie neeclidiană. În 1839, în St. Petersburg Pulkovo V. Ya Struve.
Răspunsuri la întrebările examenului privind istoria clasei Rusiei 9. Surse: Răspunsuri la întrebări / bilete la. I. Lobachevski sa aflat la sursele de geometrie neeclidiană. În 1839, în Pulkovo, sub. sindicate pentru muncitori, Komsomol pentru tineri, organizație pionieră pentru.
Răspunsuri la întrebări despre filozofie pentru cei care intră în școala absolventă
Răspunsuri la întrebări despre filozofia absolvenților naturali care intră în cursul postuniversitar. este sacrificată mecanicii, iar geometria este proclamată știința principală. Un merit important. al doilea plan. În clasa germană de filozofie, filozofia naturală este prezentată din nou.