Metode numerice pentru rezolvarea ecuațiilor neliniare. Metoda acordurilor.
Metoda acordurilor (metoda este, de asemenea, cunoscută ca metoda secantelor) este una din metodele de rezolvare a ecuațiilor neliniare și se bazează pe îngustarea succesivă a intervalului care conține rădăcina unică a ecuației. Procesul iterativ este efectuat până la atingerea preciziei specificate.
Spre deosebire de metoda de împărțire în două, metoda oferă coardă că împărțirea intervalului nu se efectuează în mijloc și la punctul de intersecție al coardei cu abscisa (axa - X). Trebuie remarcat faptul că, în lungimea medie a corzii, care are loc prin punctele funcției la capetele intervalului. Metoda Privite oferă o determinare rapidă a rădăcinii decât metoda de împărțire în două, cu condiția același interval de referință luate în considerare.
Din punct de vedere geometric, metoda corzii este echivalentă cu înlocuirea curbei cu o coardă care trece prin punctele u (vezi figura 1).
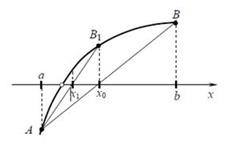
Fig.1. Construirea unui segment (coardă) unei funcții.
Ecuația liniei drepte (coardă) care trece prin punctele A și B are următoarea formă:
Această ecuație este o ecuație tipică pentru descrierea sistemului direct de coordonate carteziene. Panta curbei este dată de ordonată și de abscisă folosind valorile din numitor și. respectiv.
Pentru punctul de intersecție al liniei cu axa abscisei, ecuația scrisă mai sus va fi rescrisă în următoarea formă:
Ca un nou interval pentru procesul iterativ, alegeți una dintre cele două sau. la capetele cărora funcția ia valori de semne diferite. Opusul semnelor valorilor unei funcții la capetele unui segment poate fi determinat în mai multe moduri. Unul dintre mai multe dintre aceste metode - multiplicarea valorilor de la punctele finale și definiția produsului prin compararea semnului rezultatului înmulțirii la zero:
Procesul iterativ de rafinare a rădăcinilor rădăcinii atunci când starea de proximitate a două aproximări succesive devine mai mică decât precizia specificată, adică
.
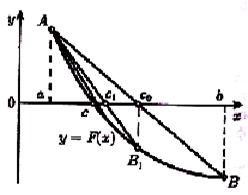
Fig.2. Explicație la determinarea erorii de calcul.
Trebuie notat faptul că convergența metodei acordurilor este liniară, dar mai rapidă decât convergența metodei de divizare divizată.
Algoritmul pentru găsirea rădăcinii unei ecuații neliniare prin metoda acordurilor
1. Găsiți intervalul inițial de incertitudine prin una dintre metodele de separare a rădăcinilor. Setați eroarea de calcul (un număr pozitiv mic) și pasul inițial al iterației ().
2. Gasiti punctul de intersectie al coardei cu axa abscisa:
3. Este necesară găsirea valorii funcției la puncte. și. Apoi, trebuie să verificați două condiții:
- dacă condiția este îndeplinită. atunci rădăcina dorită se află în interiorul segmentului stâng. ;
- dacă condiția este îndeplinită. atunci rădăcina dorită este în interiorul segmentului din dreapta pentru a lua. .
Ca rezultat, există un nou interval de incertitudine pe care se găsește rădăcina dorită a ecuației:
4. Verificăm valoarea aproximativă a rădăcinii ecuației pentru o precizie dată, în cazul:
- Dacă diferența dintre două aproximări succesive devine mai mică decât precizia specificată. atunci procesul de iterație se termină. Valoarea aproximativă a rădăcinii este determinată de formula:
- Dacă diferența a două aproximări succesive nu atinge precizia necesară. atunci este necesar să se continue procesul iterativ și să se continue la etapa 2 a algoritmului în cauză.
De exemplu, ia în considerare soluția unei ecuații neliniare prin metoda acordurilor. Rădăcina trebuie găsită cu precizie în intervalul examinat.
Soluția ecuației neliniare din pachetul software MathCAD.

Rezultatele calculelor, și anume dinamica modificării valorii aproximative a rădăcinii, precum și eroarea de calcul din etapa de iterație sunt prezentate în formă grafică (vezi figura 1).
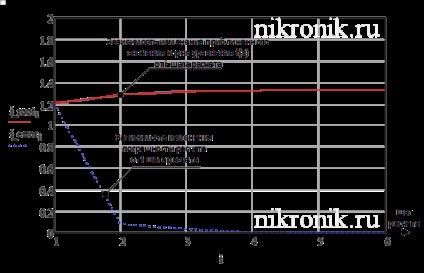
Fig.1. Rezultatele calculului prin metoda acordurilor
Pentru a asigura precizia specificată atunci când căutați o ecuație în domeniu, este necesar să efectuați 6 iterații. La ultima etapă a iterației, valoarea aproximativă a rădăcinii ecuației neliniare va fi determinată de valoarea :.
O modificare a acestei metode este o metodă de poziție falsă (False Poziția Method), care diferă de metoda secantă doar prin faptul că nu de fiecare dată luat ultimele 2 puncte, și acele puncte care sunt în jurul rădăcinii.
Trebuie notat că dacă al doilea derivat al algoritmului de căutare poate fi simplificat de la o funcție neliniară. Să presupunem că al doilea derivat păstrează un semn constant și ia în considerare două cazuri:
Din prima condiție se dovedește că partea fixă a segmentului este partea a.
Din cea de-a doua condiție rezultă că partea fixă a segmentului este partea b.
În general, pentru a identifica sfârșitul fix, putem scrie următoarea condiție :. unde sau.
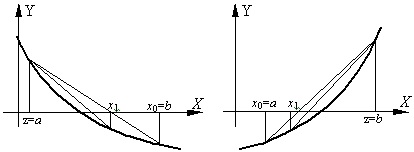
Fig. 3. Exemple de funcție descrescătoare sau de creștere
Astfel, în funcție de tipul funcției, se obțin două expresii pentru a simplifica căutarea rădăcinii funcției:
- dacă funcția corespunde cu primul caz (a se vedea figura 3), atunci formula va avea următoarea formă:
- dacă funcția corespunde celui de-al doilea caz (vezi Figura 3), atunci formula va avea următoarea formă:
Cazul se reduce la cel în cauză. dacă ecuația este scrisă sub forma :.