În această metodă, funcția neliniară f (x) pe un spațiu separat
[a, b] este înlocuit de o coardă care trece prin punctele (a, f (a)) și (b, f (b))
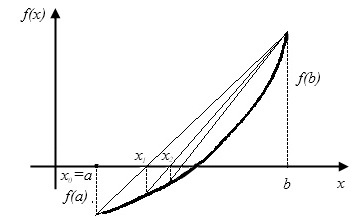
Fig.2.4. Metoda acordurilor. Capătul drept al decalajului b este staționar
Ecuația unui coardă :. Să găsim punctul de intersecție a coardei cu axa orizontală. Presupunând și. avem
Punctul x1 este considerat ca fiind noua limită a segmentului în care este conținută rădăcina. Prin acest punct cu coordonatele (x1, f (x1)) și limita corespunzătoare intervalului anterior (b, f (b)), redăm din nou o coardă, găsim etc. obținerea unei secvențe x1, x2, x3, ... xn, ... convergând la rădăcina ecuației.
Al doilea derivat păstrează un semn constant. În consecință, sunt posibile două cazuri. Dacă f (b) # 903; f "(b)> 0 atunci coarda are un capăt fix fix și secvența x0, x1, ... xn se apropie de rădăcina din stânga.Pentru aproximația inițială x0,
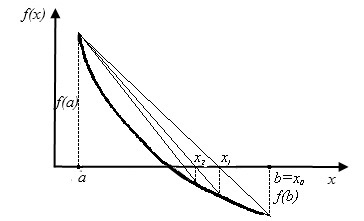
Figura 2.5. Metoda acordurilor. Capătul din stânga al decalajului a este staționar
Dacă f (a) # 903; f "(a)> 0, atunci coarda are un capăt fix stâng și secvența x0, x1, ... xn ... se apropie de rădăcina din dreapta. Pentru aproximația inițială x0,
Pentru a estima precizia, putem folosi formula
unde este rădăcina rădăcinii, este rădăcina aproximativă. pe intervalul [a, b]. Numărăm până când condiția este îndeplinită. Dacă există o inegalitate. atunci contul poate fi terminat când.
Exemplul 2.4. Găsiți rădăcina ecuației prin metoda chordului x 4 -x-1 = 0
Gasim solutia folosind pachetul Mathcad.
Funcția este monotonă pe intervale (-∞, 0.63), (0.63, ∞) și modifică semnul la capetele intervalelor. Ecuația are două rădăcini. Restricționăm intervalele de separare a rădăcinilor prin metoda probelor, adică substituție.