ALOCARE 7. Găsiți volumul corpului delimitat de suprafețele indicate.
Oferim o soluție de două probleme pentru calcularea volumului de corpuri, având în vedere corpurile cu geometrii de suprafață diferite.
1). Corpul este limitat de două suprafețe: un paraboloid și un avion. Desenați acest corp în desen (figura 75).
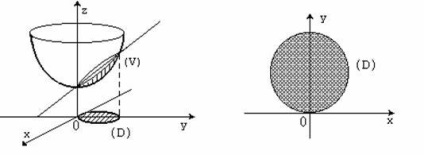
Acest corp este o rază cilindrică (figura 72); suprafața laterală a degenerat într-o linie de intersecție a suprafețelor date. Să găsim regiunea în care corpul este proiectat pe un plan, pentru care este necesar să excludem variabila (de exemplu, să efectuăm proiecția ortogonală) de la ecuațiile suprafețelor care au legat corpul:
Astfel, regiunea () este un cerc cu centrul în punctul (0; 1) cu raza = 1 (vezi Fig. 75).
Volumul corpului poate fi calculat cu ajutorul integrala tripla prin formula. În sistemul de coordonate carteziene, integrarea triplă este scrisă repetată după cum urmează:
din care se poate observa că calculul său este asociat cu dificultăți considerabile (în etapa finală de calcul al integralității repetate).
Scriem integrala într-un sistem de coordonate cilindrice cu care sistemul cartezian este legat de formule
Transformarea iacobiană. Formula de tranziție (în integral) are forma
Scriem ecuațiile paraboloidului și planului într-un sistem de coordonate cilindrice:
Pentru cercul pe care îl avem; Este evident că unghiul trebuie să fie schimbat de la 0 la. În acest fel,
Bara cilindrică este proiectată pe plan într-un trapez curbil (D): 0 # 61603; # 61472; x # 61603; # 61472; 1, 0 # 61603; # 61472; y # 61603; # 61472; . Transformăm integralele triple într-un integrat repetat și calculăm:
Notă. În sistemul de coordonate cilindrice, calculele sunt simplificate:
ALOCARE 11. Calculați integritatea curbilinie
prin formula lui Green; Conturul închis () este compus din două curbe: u (vezi figura 80).
ASCULTARE 12. Calculați masa arcului curbei () pentru o densitate dată:
1) Se ia în considerare cazul specificării parametrice a curbei (). Masa unei curbe de avion poate fi calculata cu ajutorul unui integrala curbilinie a primului tip :. Pentru a calcula aceasta, este necesar să o reducem la un integral integrat al unei funcții a unei variabile de-a lungul unui interval de formula:
Lucrarea de forță asupra deplasării unui punct material al masei unității este un integrator liniar de-a lungul arcului de la un punct la altul
Ultimul integral este un integrator curbilinar al celui de-al doilea tip de-a lungul curbei spațiului. Calculul său se reduce la calculul unui integral definit, pentru care curba trebuie reprezentată în formă parametrică (condiția problemei este dată de curba intersecției suprafeței unui cilindru circular cu un plan, vezi Fig. 81).
Un exemplu. Să găsim unde este modulul vectorului de rază.
Prin formula 5, această egalitate presupune:
Am obținut o formulă pentru calculul funcției radiale a funcției radiale.
Considerăm acum suprafața plană a unui câmp scalar, adică suprafața dată de ecuație. Să presupunem că este o funcție continuă diferențiată. Apoi ecuația planului tangent într-un punct situat pe această suprafață are forma.
Coordonatele vectorului de gradient sunt coeficienții acestei ecuații. Prin urmare, planul normal până la planul tangent în m și, prin definiție, suprafața normală la nivelul nivelului în acest punct.
Fluxul vectorului prin suprafață. Divergența unui câmp vectorial. Fie un câmp vectorial, să fie o suprafață cu două laturi. Lăsați partea selectată, adică normal. O numim fluxul vectorului prin suprafață până la partea indicată.
Acest termen coincide cu următoarea problemă hidrodinamică. Fie vectorul vitezei fluxului de fluid la un moment dat. Calculați cât de mult lichid va trece printr-o mică parte a suprafeței la un moment dat. Acest volum de lichid este un cilindru cu o bază și o înălțime, adică acest volum este egal cu.
Apoi pentru întreaga suprafață pe care o obținem. Astfel, fluxul este rata de schimbare a cantității care curge prin lichid la momentul de timp.