Astfel, concentrația purtătorului în semiconductori intrinseci și impurități depinde puternic de temperatură. Unul dintre parametrii principali care caracterizează gazul purtătorilor liberi în semiconductori este nivelul Fermi, care depinde și de temperatură.
În semiconductoare intrinseci și slab dopate, spre deosebire de metale, gazul de electroni este nondegenerat și poate fi descris de statisticile clasice Maxwell-Boltzmann.
La o temperatură T (T> 0 K), electronii sunt în banda de conducție a unui astfel de semiconductor, iar găurile sunt în banda de valență. Denumiți concentrațiile lor cu n și respectiv p. Să luăm fundul benzii de conducere ca origine a energiei electronilor. Folosind relațiile obținute anterior (3.3) pentru funcția Maxwell-Boltzmann, este posibil să se determine numărul de particule în intervalul E. E + dE ca
În semiconductorii nedegenerați, EF este negativ și, prin definiție, este sub fundul benzii de conducție (figura 5.3a).
Denumim distanța de la vârful benzii de valență la nivelul Fermi ca # 956; ', iar distanța de la nivelul Fermi până la partea inferioară a benzii de valență - # 956; (Figura 5.3, a).
Din figura aceasta rezultă
unde Eg este lățimea benzii interzise a semiconductorului.
Fig. 5.3. Structura banda a semiconductorului: a - constantă de temperatură;
Numărul total de electroni din banda de conducere poate fi determinat prin integrarea (5.33) în intervalul de la 0 la E2. Deoarece funcția exp (-E / kT) scade foarte rapid, limita superioară a integrării E2 (aici nu negativă) poate fi înlocuită aproximativ la infinit, astfel încât
Calculul acestui integral duce la următorul rezultat:
unde NC este densitatea efectivă a stărilor din banda de conducere.
Un calcul similar efectuat pentru densitatea găurilor din banda de valență conduce la expresie
unde NV este densitatea efectivă a stărilor din banda de valență.
Rezultă din (5.36) și (5.37) că concentrația purtătorilor de sarcină liber într-o anumită zonă este determinată de distanța acestei zone față de nivelul Fermi: cu cât este mai mare această distanță, cu atât concentrația purtătorului este mai mică.
În semiconductorii intrinseci, concentrația de electroni în banda de conducție ni este egală cu concentrația gaurilor din banda de valență
Ecuând laturile drepte ale lui (5.36) și (5.37) și rezolvând ecuația rezultantă în raport cu EΦi, cu acordul pentru (5.34), obținem expresie
Ultima relație determină poziția nivelului Fermi în semiconductori intrinseci. La zero absolută (T = 0)
și anume Nivelul Fermi este situat în mijlocul benzii interzise (Fig 5.3, b). Pe măsură ce crește temperatura, se schimbă fie în sus (mp *> mn *), fie în jos (mp * Înlocuind EFi de la (5.39) în (5.36) și (5.37), obținem o expresie care descrie concentrația purtătorilor de sarcină în semiconductori intrinseci Analiza acestei expresii arată că concentrația purtătoare de echilibru în semiconductor este determinată de decalajul de banda de semiconductoare și temperatura. Această dependență este foarte puternică. Astfel, o scădere de la 1,2 eV Eg (siliciu) la 0,08 eV (staniu gri) la temperatura camerei conduce la o creștere a concentrației de 9 ordine de mărime, și creșterea germaniu temperaturii de la 100 K la 600 K, purtătorul de concentrare crește cu 17 ordine de mărime. Cu toate acestea, semiconductorii sunt adesea utilizați într-o versiune de impurități, adică cu includerea impurității donatorului sau a acceptorului (secțiunea 4.6). Reamintește că, în acest caz, semiconductorii au o concentrație mai mare de purtători de sarcină, în special la temperaturi scăzute. La temperaturi scăzute, energia medie a vibrațiilor termice ale rețelei de cristal este mică și insuficientă pentru a transfera electronul prin banda interzisă. Cu toate acestea, această energie poate fi suficientă pentru tranziții: nivelul donatorului - banda de conducere; sau banda de valență - nivelul acceptorului, deoarece # 916; <<Еg или ΔЕа <<Еg . Поэтому при низких температурах в примесных проводниках происходит возбуждение практически лишь примесных уровней. Putem presupune că concentrația atomilor donatori ionizați în funcție de distribuția Maxwell-Boltzmann este unde Ng este concentrația atomilor din impuritatea donatorului, și concentrația de ioni ale impurității acceptoare este În cazul temperaturilor scăzute, conform legii conservării încărcării, respectiv pentru semiconductorii cu electroni și gauri, putem scrie Ecuating (5.37) și (5.42), obținem expresii pentru nivelul Fermi într-un semiconductor cu electroni Rezultă din (5.45) că la temperatura zero nivelul Fermi se află în mijlocul intervalului Eg + Ec = Ed și se deplasează în jos cu creșterea temperaturii (Figura 5.4, a). Dacă reprezentăm ultima expresie din (5.37), obținem o formulă pentru concentrația principalilor purtători (electroni) în n-semiconductor De asemenea, este interesant să găsim concentrația transportatorilor minoritari în găurile de semiconductori electronice pn. Pentru a face acest lucru, trebuie să înlocuim expresia pentru nivelul Fermi (5.45) în (5.38). După o serie de transformări simple, obținem legea masei efective Din această lege rezultă că, odată cu creșterea concentrației impurității donatorilor și, în consecință, cu creșterea concentrației principalilor transportatori, se observă o scădere a concentrației transportatorilor minoritari. Legea masei efective este valabilă pentru orice semiconductor nondegenerat în condiții de echilibru termodinamic. Astfel, pentru un semiconductor cu gaura putem scrie expresie Pe măsură ce temperatura semiconductorului crește, concentrația purtătorului (figura 5.4) crește până când se apropie de concentrația de impurități. În acest caz, condiția de electroneutralizare ia forma nn = Nd. Substituind formula (5.36) în această ecuație, după transformări simple obținem o expresie pentru nivelul Fermi într-un interval de temperatură dat O creștere suplimentară a temperaturii va duce la o creștere a concentrației purtătorului datorită excitației sale din banda de valență și, de asemenea, la creșterea transportatorilor minoritari. Dacă concentrația orificiilor este apropiată de concentrația de electroni, semiconductorul va fi, prin proprietățile sale, apropiat de cel pur, adică p ≈ n, Efn ≈ Efi. Argumente și calcule similare pot fi făcute pentru un semiconductor de tip p. având doar o impuritate acceptoare. În acest caz, putem scrie expresia pentru nivelul Fermi și expresia pentru concentrarea principalilor operatori de transport Expresiile (5.45), (5.46), (5.50) și (5.51) pot fi ilustrate prin graficele corespunzătoare (Figura 5.4).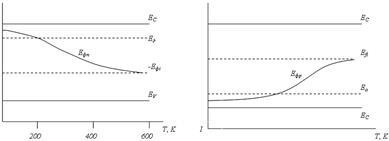
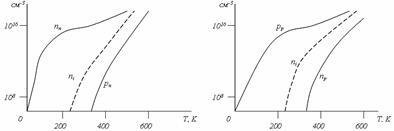
Fig. 5.4. Dependența concentrației purtătorilor de sarcină și a nivelului Fermi la temperatură:
a este un semiconductor electronic; b - un semiconductor cu orificiu
Figura arată că, la temperaturi scăzute, nivelul Fermi se află între nivelul impurităților și marginea celei mai apropiate zone. Concentrația principalilor purtători crește brusc cu creșterea temperaturii. Apoi vine regiunea în care concentrația principalilor purtători este practic constantă, iar nivelul Fermi se schimbă tot timpul până la mijlocul benzii interzise. Această regiune este numită regiunea epuizării impurităților, deoarece toți atomii disponibili sunt ionizați. La sfârșitul acestei regiuni, tranzițiile de electroni de la banda de valență la banda de conducție încep și concentrația transportatorilor minoritari crește brusc.
Dacă semiconductorul conține ambele tipuri de impurități (donatori și acceptori), atunci tipul de conductivitate este determinat de cel predominant. Dacă, de exemplu, concentrația donatorului este mai mare decât concentrația de acceptori, atunci la T = 0 toate nivelele acceptoare vor fi umplute cu electroni care au trecut de la donatori. Condiția de electricitate în acest caz are forma
unde pd este determinat anterior de la (5.42) și n - de la (5.36).
Pe măsură ce crește temperatura, toate nivelele donatorilor sunt golite și concentrația de electroni devine constantă și egală
Toate argumentele anterioare se referă la semiconductorii slab dopata, în care se aplică statisticile Maxwell-Boltzmann. Totuși, într-o serie de cazuri se utilizează semiconductori cu o concentrație mare de impurități, adică semiconductori puternic dopați.
În Fig. 5.5a arată dependența de temperatură a concentrației de electroni la diferite concentrații ale impurității donatorului Nd. Creșterea Nd determină o deplasare naturală a graficelor în sus, o creștere a temperaturilor de diminuare a impurităților și o scădere a înclinării secțiunilor de impurități ale grafurilor, adică o scădere a energiei de ionizare a impurității # 916;
Acest lucru apare și în semiconductorii acceptori. De exemplu, în siliciu dopat cu bor, schimbarea Ea cu creșterea lui Na este descrisă de relația empirică
unde Ea0 ≈ 0,08 eV este energia de ionizare în semiconductorii slab dopata;
# 945; = 4,3 # 8729; 10-10 eV / m.
În conformitate cu (5.54) cu Na = 6 # 8729; 10 24 m -3. Ea = 0 și concentrația purtătorului în regiunea de impurități încetează să depindă de temperatură. Astfel de semiconductori se numesc degenerați.
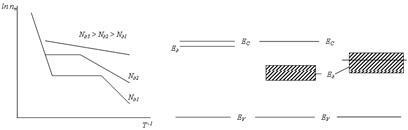
Fig. 5.5. Semiconductoare dopate: a este dependența de temperatură a concentrației
mass-media; b - nivelul impurității în banda interzisă; c - banda de impurități în banda interzisă; r este suprapunerea benzii de impuritate și banda de reductibilitate în semiconductorii degenerați
Reducerea impurităților de energie de ionizare în timp ce creșterea concentrației Npr sale, deoarece odată cu creșterea distanței dintre nPR atomilor de impuritate scade, iar interacțiunea dintre ele crește. La atingerea unei valori anumit nivel Npr impuritate este împărțită în regiunea impuritatea (fig. 5.5), și de o creșterea în continuare nPR creșteri de bandă de impurități și se poate suprapune cu banda de conducție (Fig. 5,5 g). În acest caz, energia de ionizare este zero și regiunea impurități în semiconductor se comportă practic, ca de metal. Nivelul Fermi cu creșterea gradului de dopaj banda de impuritate este deplasată la, și (în cazul unui semiconductor degenerat) apare, în funcție de tipul de impuritate, banda de conducție sau de valență. În regiunea conductivității intrinseci a unui semiconductor, concentrația purtătorilor săi dobândește din nou o caracteristică caracteristică.