9.2.1. Aplicarea metodei de tăiere a planurilor cu
În Fig.9.3. con și emisfera.
În
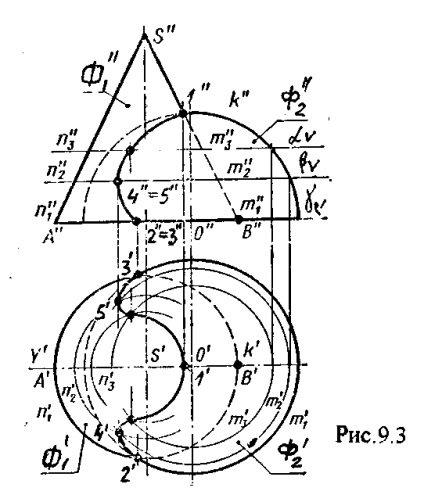
Pentru a începe construcția liniei de intersecție, este necesară începerea construcției liniei de intersecție, este necesar să se găsească punctele de referință: cea mai mare și cea mai mică în acest caz. În alte cazuri, acesta poate fi cel mai din stânga sau cel mai drept. Intersectăm ambele suprafețe cu planul V și suprafețele care trec prin axa de rotație. Ca rezultat, obținem linii de intersecție, care sunt schițe frontale ale acestor suprafețe. Punctul de intersecție al schițelor 1 este un punct care aparține liniei de intersecție.
Deoarece bazele ambelor suprafețe se află în același plan, punctele de intersecție ale cercurilor 2 și 3 sunt de asemenea puncte comune pentru aceste suprafețe.
Punctele 1,2,3 sunt punctele de referință, punctul 1 este cel mai ridicat, punctele 2, 3 sunt cele mai scăzute. Acum, atât transversale plane de suprafață, situate sub punctele de mai sus 1 și 2 și 3. Acest plan intersectează ambele suprafețe ale cercurilor n2 și M2 găsi puncte de intersecție a cercurilor obținute m2 = n2 n2 4. m2 = 5.
Punctele 4,5 aparțin liniei de intersecție a conului și a emisferei. Dacă repetăm această acțiune, de câte ori este necesar, construim o linie de intersecție a acestor suprafețe.
9.3. Metoda de sfere concentrice
În
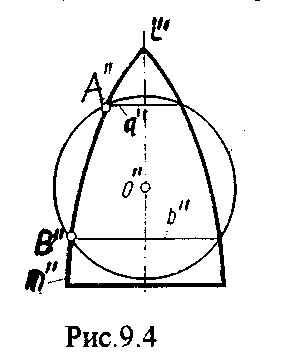
Aplicarea acestei metode se bazează pe următoarea proprietate: Două suprafețe de rotație având o axă comună (suprafețe coaxiale) se intersectează de-a lungul cercurilor. Într-adevăr, curba m formează o suprafață de rotație cu axa de rotație i, curba n formează o a doua suprafață de rotație cu aceeași axă i. Dacă mλείαn = A, atunci punctul A va descrie un cerc comun pentru ambele suprafețe, deci este linia intersecției lor. (Figura 9.4).
Dacă axa i este perpendiculară pe planul H, atunci cercul descris de punctul A este proiectat pe planul frontal al proeminențelor în segment și pe planul orizontal în cerc.
Din ceea ce sa spus, se pot trage următoarele concluzii:
1. Pentru ca sfera secantară auxiliară să se intersecteze cu două suprafețe de rotație date de-a lungul cercurilor, centrul sferei trebuie să stea în punctul de intersecție al axelor acestor suprafețe.
2. Dacă axele suprafețelor de rotație date sunt paralele cu planul proiecțiilor, atunci cercul de intersecție a sferei secante auxiliare cu aceste suprafețe este proiectat pe acest plan în segmente.
Acum putem formula condițiile necesare pentru aplicarea metodei sferelor concentrice secante:
1. Datele de suprafață trebuie să fie suprafețe de rotație;
2. Axele de rotație ale acestor suprafețe trebuie să se intersecteze;
3. Planul care trece prin axa de rotație a acestor suprafețe trebuie să fie paralel cu un anumit plan de proiecție.
Construcția liniei de intersecție începe cu construirea punctelor de control (Fig.9.5). Pentru a construi punctele de sprijin, trebuie să construim o sferă de rază minimă. Sfera razei minime este înscrisă într-o singură suprafață și intersectează a doua.
Punctele comune C și D ale cercului de tangență cu conul și cercul de intersecție cu cilindrul sunt punctele de referință. Punctele de referință includ, de asemenea, punctele de intersecție ale schițelor frontale ale acestor suprafețe. Segmentul OffsFigure unde punctul de intersecție al schițelor acestor suprafețe cel mai îndepărtate de punctul O determineat determină sfera razei maxime.
Pentru a construi puncte intermediare, este necesar să alegem o sferă de rază R, unde Rmin este o elipsă