Stocarea structurilor ierarhice folosind modelul de seturi imbricate
Modelul părinte-copil
În mod tradițional, structura ierarhică este un model în care relația dintre părinți și descendenți este monitorizată în mod clar. În cazul unei structuri arborice, fiecare nod va avea un ID unic și ID-ul părintelui. ID-urile în sine nu au nimic de-a face cu datele, toate servesc drept identificatori de noduri unici. Rădăcina copacului trebuie să aibă o valoare specială pentru ID-ul nodului părinte, deoarece rădăcina părintelui nu există.
Luați în considerare următoarea schemă:
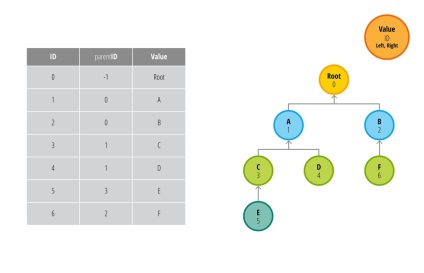
Fiecare săgeată indică paternitatea nodului în conformitate cu valorile ID. numele părintelui și valoarea din tabel. Acest model este folosit cel mai adesea pentru a reprezenta structuri ierarhice. Fiecare nod are informații despre părinte și descendenți.
Din păcate, există probleme care utilizează acest model dacă vrem să îi luăm pe toți copiii unui singur nod. Să presupunem că avem nevoie pentru a obține un act de identitate pe toate nod element de copil cu un ID de 1. Privind la graficul nostru, putem spune cu siguranță că acest lucru este nodurile 3, 4 și 5. Cu toate acestea, atunci când se utilizează un tabel de baze de date pentru a face nu atât de ușor.
Obținerea nodurilor copilului
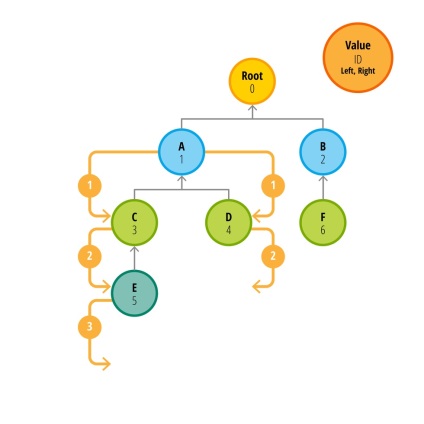
În primul rând obține toate nodurile părinte al căror nod ID-ul este setat la 1. În acest caz, nodurile 3 și 4 (săgețile galbene pe figură arată numărul cererii la PB). Acum avem pentru a obține copii ale unităților 3 și 4. Nu este dificil de a vedea că această metodă va duce la sute sau chiar mii de interogări la baza de date prin utilizarea unei cantități mari de date. Rețineți că numărul de interogări solicitate este proporțional cu înălțimea arborelui. Întotdeauna trebuie să efectuăm o interogare mai mult decât înălțimea arborelui de date.
Seturi netede - soluția problemei (set de nivelare)
Aici vine ideea de seturi încorporate. Acest model nu este la fel de simplu ca cel precedent, așa că să încercăm să ne dăm seama împreună. În locul identității părintelui, vom stoca valorile valorilor stânga și dreapta ale nodului. Uită-te la masă și diagrama de mai jos:
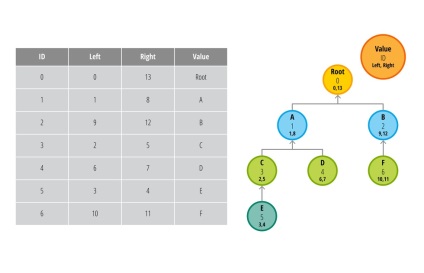
Asta e, nu? Ce sa întâmplat?
Deci, calm. Să ne întoarcem un pas și să ne dăm seama cum sa întâmplat. Valorile stânga și dreapta stochează referințele la nodurile copilului. La rândul lor, nodurile copilului au, de asemenea, astfel de variabile, prin urmare definiția seturilor imbricate. De exemplu, dacă am avea nevoie să obțin toate elementele copilului nodului A (ID = 1), aș executa următoarea interogare:
Ca răspuns, aș primi nodurile C, D și E. Rețineți că am făcut fără recurs, am avut doar o singură cerere.
Totul este bine, dar cum definiți valorile stânga și dreapta ale copacului construit?
În mod surprinzător, acest lucru nu este deloc dificil. Iată schema algoritmului acestei proceduri:
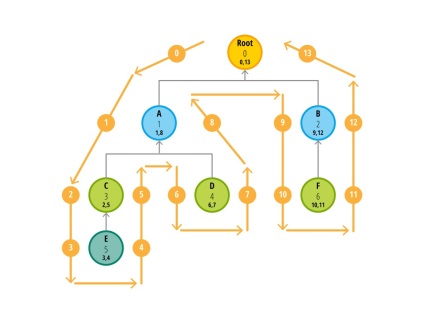
Definirea valorilor din dreapta și din stânga
Începeți cu săgeata din stânga sus și contorul egal cu 0. Pe măsură ce treceți nodul, măriți contorul cu 1 și introduceți-l în nod. Dacă sunteți în stânga nodului, atunci valoarea contorului este lăsată. și dacă ești pe dreapta, atunci bine.
Rețineți că, dacă acest nod nu are elemente copil, valorile din stânga și din dreapta diferă de unul, și dacă există, diferența în valorile de cel puțin trei, și adâncirea crește cuibărit de două. Aceste informații ne indică multe lucruri fără a folosi solicitări suplimentare la baza de date.
Vedere alternativă
Să încercăm să analizăm mai atent această structură a datelor:
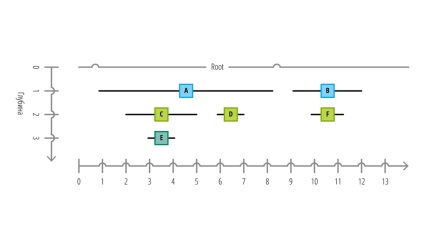
Dintr-o astfel de schemă, putem determina cu ușurință structura seturilor și adâncimea cuiburilor lor (distanța față de rădăcină). Linia de coordonate inferioară reprezintă o dimensiune, în care sunt localizate toate nodurile. ID-ul fiecărui nod următor este incrementat de unul, iar fiecare nod are un buffer pentru stocarea datelor. Dacă am mai făcut o solicitare de a primi toți copiii din nodul A, atunci cererea noastră ar lua forma următoare:
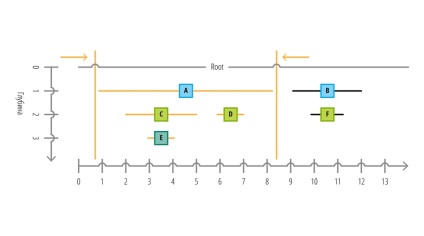
Adăugarea de noduri
Să adăugăm un nou nod cu o valoare de G imediat după rădăcina arborelui (nodul rădăcină). Uită-te la masă și diagrama de mai jos:
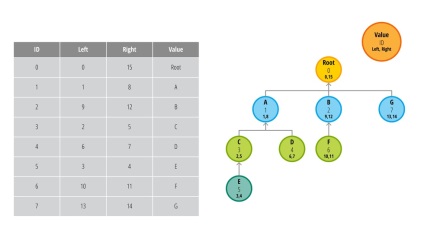
Pentru a adăuga un nod ca un copil direct al unui alt nod, trebuie mai întâi să alocați spațiu în arbore. Pentru a face acest lucru, obținem valoarea corectă a nodului sursă. În cazul nostru, acesta este 13. Pentru a selecta spațiul necesar, adăugați 2 la toate valorile din dreapta și din stânga. care sunt mai mult de 13.
Din moment ce adăugați un nod imediat după rădăcină, actualizarea valorilor din stânga nu este necesară (vom adăuga nodul G ca succesor al rădăcină spre dreapta, pentru a minimiza numărul de interogări la baza de date. Încercați să adăugați în partea stângă a nodului și a vedea cât de multe valori pe care le va trebui să actualizați). După ce ați alocat spațiul necesar, adăugați nodul, specificând valoarea stânga egală cu cea din dreapta nodului și valoarea corectă egală cu aceeași valoare plus una.
Cum să ștergeți nodurile?
Ștergerea nodurilor este o operație foarte simplă. Să analizăm mai multe opțiuni posibile:
Eliminarea nodului final (care nu are copii)
Ștergeți nodul final, iar restul copacului rămâne neschimbat
- Reduceți toate valorile stângi cu 2, care este mai mare decât valoarea stângă a nodului la distanță
- Reduceți toate valorile corecte cu 2, care este mai mare decât valoarea corectă a nodului la distanță
- Ștergeți singur nodul
Ștergerea unui nod cu copii
- Reduceți valorile stânga și dreapta cu una dacă valoarea stângă este mai mare decât valoarea stângă a nodului care este șters, iar valoarea corectă este mai mică decât valoarea corectă.
- Reduceți toate valorile stângi cu 2 dacă acestea sunt mai mari decât valoarea stângă a nodului care este șters.
- Reduceți toate valorile corecte cu 2, dacă acestea sunt mai mari decât valoarea corectă a nodului șters.
- Scoateți nodul.
Eliminarea nodului rădăcină
Se pare, de asemenea, ștergerea unui nod cu copii, cu excepția faptului că, în final, nu putem obține decât unul, dar mai mulți copaci. Dacă rădăcina avea mai mulți descendenți, atunci în final ei devin noduri rădăcină. De obicei, acest lucru nu este foarte bun, dar uneori acest comportament este necesar.
Dezinstalați exemplul
Să vedem cum arată ștergerea unui nod cu copii (nod A, index 1):
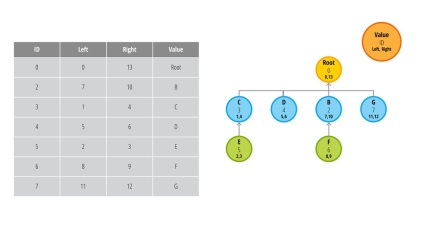
Notă, nodurile C și D devin copii ai nodului rădăcină, iar nodul E a fost un descendent al lui C. Dacă am fi continuat, și ștergeți nodul rădăcină, v-ar fi primit ca rezultat al nodului rădăcină 4 și 2 copii (de obicei, rezultatul este o eroare, dar din nou, totul depinde din sarcină).
eficacitate
Seturile neregulate sunt foarte eficiente atunci când regăsiți lista de copii a unui element. Dar există unele dezavantaje, de exemplu, atunci când ștergeți sau adăugați un nod, acest model pierde, deoarece este necesar să efectuați un număr mare de actualizări ale bazei de date. Chiar dacă gestionați doar trei interogări SQL pentru a insera o intrare, numărul de cereri de actualizare a unui nod poate fi destul de mare, ceea ce poate afecta viteza bazei de date.