Prin scăderea simplă este ușor de verificat valabilitatea
Adăugând un număr la ambele părți ale acestei ecuații, obținem o nouă egalitate
în care, așa cum nu este greu de văzut, părțile din dreapta și din stânga sunt pătrate complete,
Extragând rădăcina pătrată din partea dreaptă și cea stângă a egalității anterioare, obținem egalitatea:
din care rezultă că
Prin definiție, este un anumit număr ne-negativ, care, atunci când este pătrat, dă. Este clar că acest număr este satisfăcut de două numere, și anume x și -x. Deci, dacă numărul x este non-negativ (x> 0), atunci = x; dacă numărul x este negativ, adică numărul -x este pozitiv, apoi = - x. Din aceasta conchidem că (proprietatea unei rădăcini aritmetice pătrată), care nu este luată în considerare în conținutul acestor sofisme și conduce la concluzii false.
"Fiecare număr este egal cu jumătatea lui".
Se scrie identitatea a2-a2 = a2-a2, evidentă pentru orice număr a, unde a este orice număr.
Așezați-o pe partea stângă a suportului și împărțiți partea dreaptă cu un factor în funcție de formula diferenței de pătrate, obținem un (a - a) = (a + a) (a - a).
Împărțirea ambelor părți cu a - a. obținem a = a + a. sau a = 2a.
Împărțim cu 2 și obținem a = a / 2
Împărțim ambele părți cu zero, iar împărțirea cu zero este interzisă.
"Două perpendicule pot fi aruncate printr-un punct pe o linie dreaptă"
Vom încerca să "dovedim" că printr-un punct situat în afara unei linii drepte, două perpendicule pot fi trase la această linie. În acest scop, luăm triunghiul ABC. Pe laturile AB și BC ale acestui triunghi, ca și pe diametre, construim semicercuri. Să aceste semicercuri se intersectează cu AC lateral, la punctele E și D. se alăture punctele E și D cu punctul B. drept Unghiul AEB drept ca înscris, în funcție de diametrul; unghiul VAB este, de asemenea, drept. În consecință, BE este perpendiculară pe AC și BD este perpendiculară pe AC. Două perpendiculare la linia dreaptă trece prin punctul B.
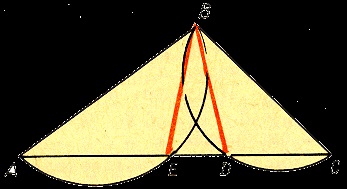
Argumentele potrivit cărora două perpendicule pot fi scoase dintr-un punct pe o linie se bazează pe un desen eronat. În realitate, semicercurile se intersectează cu partea de AS la un moment dat, adică BE coincide cu BD. Prin urmare, dintr-un punct pe o linie dreaptă două perpendicule nu pot fi scăpate.
Fiecare număr pozitiv este negativ.
Fie n un număr pozitiv.
Luăm un alt număr pozitiv arbitrar și multiplicăm ambele părți ale inegalității cu (-a): -2an + a<-2an.
Dacă deducem cantitatea (-2an) de ambele părți ale acestei inegalități, obținem inegalitatea a<0, доказывающее, что всякое положительное число является отрицательным.
Atunci când se înmulțește cu un număr negativ, semnul inegalității se modifică.