În Fig. 12 prezintă aplicarea unei antene cu dublă fantă de radiație înapoi, cunoscută sub numele de iradiatorul Cutler.
Cu un astfel de iradiator, sistemul de antene este compact într-un mod constructiv. Iradierea are un efect net mai mic decât alte iradiatoare.
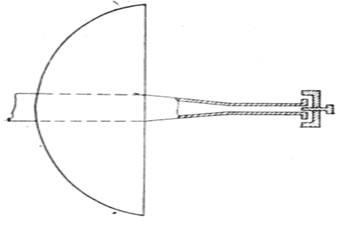
Modelul de radiație al unui astfel de iradiator depinde de lungimea și lățimea fantelor și de distanța dintre golul de pe peretele ghidului de undă. Prin urmare, poate fi reglabil și selectat în funcție de cerințe. Reglarea se face experimental.
Faza frontală a valului emis de acest iradiator este aproape sferică. Distorsiunile de fază care apar datorită reflexiei din pereții ghidului de undă nu depășesc 30 °.
Radiații de bandă largă de polarizare circulară.
În Fig. 13a-d prezintă un grup de Hublou oglinzi proiectate să funcționeze într-o lățime de bandă largă și câmp de polarizare circulară radiație creând: spirală, respectiv cilindrice, plat spirală conică spirală antenă periodică
Două oglinzi parabolice antene.
Diagrama unei antene cu două oglinzi.
Într-o serie de cazuri practice, antenele cu două oglinzi arătate schematic în Fig. 14 și 15.
antenă dublu reflector este format din iluminatorul 1, prima suprafață luminoasă a oglinzilor mici 2, prin care unda de suprafață este direcționată către oglinda mare 3. După reflexie din oglinda diafragmei sale mari creat câmp de mod comun. Vom folosi în viitor termenii "oglindă mică" și "oglindă primară" sau "oglindă primară". Alimentarea cu alimentatorul este alimentată de alimentatorul 4 de la emițător (receptorul) 5.
Procesele reradiation oglindă mică și formarea o deschidere de mijloc a oglinzii primare realizate în poziții de cale teorie antenă Tov cu optica geometrice, folosind conceptul de incident și reflectate grinzi. Atunci când suficient de mare (în lungimea de undă unitate nitsah), departe de iluminator oglinzi mici și ultimul dintre reflectorului principal, și o rază suficient de mare de curbură a ambelor oglinzi un astfel de tratament oferă o bună aproximare la valoarea adevărată. Prin urmare, se poate argumenta că unda sferică emisă din punctul central al paraboloidului, pre-oglinda este formată într-un plan, și pe baza oricărui de focalizare a hiperboloidul sau elipsoid după reradiation păstrează față de undă nyaet-sferică. În acest caz, centrul său de fază este transferat la cel de-al doilea foc al oglinzii mici. Dacă a doua focalizarea (punctul central al fazei) pentru a se combina cu focalizarea paraboloidului, după reemisia al doilea val plan este format dintr-un paraboloid. Figura 14.16b ilustrează aceste poziții utilizând exemplul unei mici oglinzi de formă hiperbolică. Mici oglindă hiper parabolic 2, 2“, 2„, pot fi trase spre convexitate parabolic pas sau concavitate 2 2' . Poziția intermediară dintre convex și hyperboloids concave-tricotat maet planul 2“. În cazul oglinzilor mici .ploskogo 2" undele sferice supraeedate au un centru de fază la distanța imaginii oglindite a punctului din centrul de fază al iradiatorului. O mică oglindă eliptică 2 "este prezentată în figura 14a, care este întotdeauna trasă la o concavitate parabolică.
Curbele din Fig. 14 b și 15 de circuit cu două oglinzi en Tenn cu convex mici și oglinzi concave în astronomice împrumutate de optică și denumite inventatori, respectiv, denumite în oglindă telescoape Cassegrain și Gregory (Cassegrain antena -. 14 și Fig antena Gregory -. Figura 15 a).
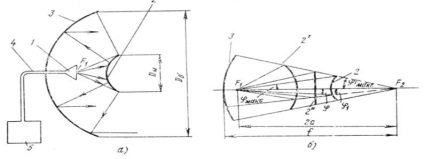
În Fig. 15 b prezintă așa-numita antenă cu o axă deplasată. Este descris mai detaliat mai jos.
Există antene cu două oglinzi, cu suprafețe sintetizate ale oglinzilor mari și mici, selectate din condiția de optimitate a caracteristicilor.
Două oglinzi antena Cassegrain.
Amintiți-vă că antena Cassegrain mare oglindă parabolică 3, și un mic (prefokalnoe) 2 - hiperbolică-TION. Acesta este plasat, așa cum se arată în Fig. 16, partea convexă a oglinzii mari. Centrul de fază al iradiatorului 1 este localizat la punctul focal fi al reflectorului hiperbolic; Al doilea focalizare F2 a hiperboloidului coincide cu focalizarea oglinzii parabolice. Valul sferic este transformată în oglindă iradiatorul mică sferică în același val, dar centrat pe F2. care, la rândul său, este transformată de o oglindă mare într-o undă plană care creează un câmp în fază în deschidere.
La calcularea antenelor cu două oglinzi, este convenabil să se utilizeze echivalentul a 4 antene parabolice cu o singură oglindă, ale cărui profil grafic pentru antena Cassegrain este ilustrat în Fig. 16. Liniile drepte paralele cu axa antenei sunt trase prin punctele extreme ale curbei a și b ale oglinzii mari; din focalizarea fi, două linii drepte trec prin marginile oglinzii mici până la intersecția în punctele a 'și b' cu liniile directe aa 'și bb'.
O parabolă cu focalizare în punctul F1 este trasă prin punctele a 'și b'. În Fig. 16 prezintă construcția grafică a acestei parabole 4.
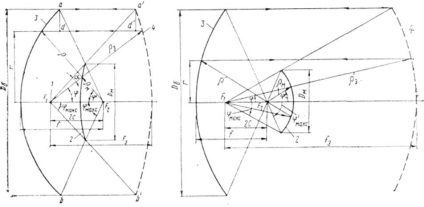
Punctele f1 și F2 sunt trase prin același punct al unei mici oglinzi a vectorilor de rază, ρ și ρ0. Din punctul de intersecție p cu o oglindă mare, o linie dreaptă paralelă cu linia dreaptă aa 'este trasă la intersecția cu ρ e. Astfel de puncte de intersecție, pentru a forma o oglindă echivalentă 4. Este ușor de văzut că antena reflector principal și parabolei echivalent în raport cu reciprocated mică oglindă hiperbola. Dacă vă construi o antenă cu două oglinzi, luând ca o oglindă mare echivalentă unei parabole, ca o mică oglindă - același hiperboloidul, dar cu care se confruntă Story concav Noe într-o oglindă mare, și plasați iradiator la F2. atunci oglinda principală a antenei va fi o parabolă echivalentă.
Orice două raze care emană un punct F1 spre parabolei equi-valent, altele - din punctul F2 spre antenă parabolică și care trec prin același punct de oglinzi mici, sunt reflectate de oglinzi mari respective pe aceeași linie de-mina unul către celălalt. Considerând fasciculul de lumină îngustă, cu o dimensiune unghiulară și se poate observa că diafragma dvuhzer Kalnoy-antenă-oglindă și o arie a secțiunii transversale echivalente a grinzilor vor fi identice (ad - a'd „) si ca-ne energie tolerabilitate prin aceste secțiuni, și unul aceleași, apoi densitățile energetice și, prin urmare, distribuțiile de amplitudine ale câmpului în ambele deschizături se dovedesc a fi identice. Acest lucru permite definirea antenei Cassegrain cu două oglinzi radiație câmp-lenii pentru a rezolva o problemă similară pentru antena echivalentă oglindă.