
Hârtie logaritmică cu coordonate numerice de la (1; 1) la (100; 100)
Hârtia logaritmică este un fel de hârtie de coordonate scară. pe care grila este construită pe o scară logaritmică. Este de obicei produs prin imprimare. Se folosește de asemenea hârtie semilogaritmică, de-a lungul căreia este așezată o scară uniformă de-a lungul unei axe, în timp ce pe cealaltă axă este logaritmică.
Sunt utilizate hărțile logaritmice și semi-logaritmice pentru a descrie graficele funcțiilor. care la o scară logaritmică iau o formă mai simplă (în unele cazuri, o linie dreaptă). Sunt convenabile pentru reprezentarea grafică a datelor care variază într-o gamă foarte largă de valori (cu mai multe ordini de mărime). Firește, argumentul și (sau) funcția. stabilite pe o scară logaritmică, ar trebui să ia doar valori pozitive.
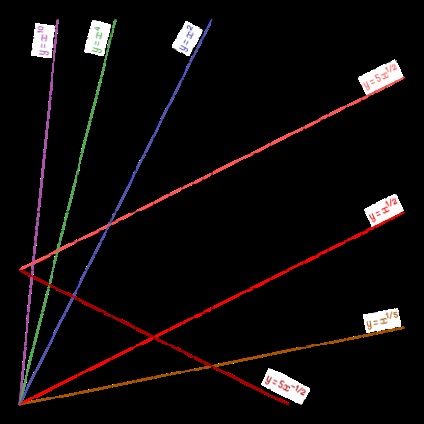
Graficele funcțiilor de putere la scară logaritmică
Pe hârtie logaritmică, forma liniilor are grafice ale funcțiilor de putere ale formulei y = a x b>. deoarece prin logaritm, dependența de putere-putere este redusă la liniară: lg y = lg a + b l g x, y = \ mathrm \, a + b \, \ mathrm \, x>. Panta liniei (coeficientul unghiului) este determinată de exponentul gradului b. Pentru b> 0, această funcție crește, iar pentru b <0 убывающая; при b = 0 прямая горизонтальна, y = a . Точка пересечения прямой с осью ординат определяется коэффициентом a. В частности, при a = 1 графики y = x b> sunt liniile care traversează originea: l g y = b l g x \, y = b \, \ mathrm \, x>.
Pe o hârtie semilogaritmică cu o scară logaritmică de-a lungul axei abscise, liniile au graficele funcțiilor logaritmice y = log b (a x) (ax)>. Coeficientul unghiular al liniei drepte este determinat de baza logaritmului b. funcția crește în cazul b> 1 și scade la 0 .
Pe o hârtie semilogaritmică cu o scară logaritmică de-a lungul axei ordonate, tipul de linii are grafice ale funcțiilor exponențiale y = a b x>. Dependența exponențială se reduce la o cale liniară a logaritmului: l g y = l g a + x l b b, y = \ mathrm \, a + x \, \ mathrm \, b>. Coeficientul unghiular al unei linii drepte este determinat de baza gradului b. funcția crește în cazul b> 1 și scade la 0 .