Pentru valori mari de n, formula lui Bernoulli este asociată cu calcule consumatoare de timp. Trebuie să calculați:
În mod evident, acest lucru este dificil din punct de vedere tehnic. În astfel de cazuri, utilizați formula, care este cazul limitator al formulei Bernoulli.
Formula locală Laplace. Dacă probabilitatea p de apariție a evenimentului A este constantă pentru fiecare test și este diferit de 0 și 1, atunci probabilitatea ca un eveniment A se produce k ori în n studii independente, un număr suficient de mare n este aproximativ egal cu
unde este funcția Gaussiană (figura 2.2).
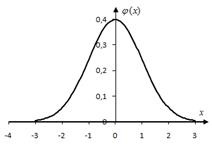
Cu cât mai mult n. cu mai multă precizie (2.3). Când dă rezultate satisfăcătoare pentru practică.
Valorile funcției Gauss sunt prezentate în Tabelul B.1 din Anexa B.
Proprietățile funcției Gaussian:
1. este o funcție uniformă; .
2. Funcția scade monotonic pentru valorile pozitive ale lui x. și la (practic se poate presupune că deja la).
Exemplul 2.3. Probabilitatea producerii unui element de calitate premium pe această mașină este de 0,4. Găsiți probabilitatea ca printre cele 56 de articole luate aleatoriu, jumătate să fie de cea mai înaltă calitate.
Soluția. n mare ,. prin urmare, aplicăm formula locală Laplace (2.3). Realizăm calculele necesare:
Următoarea formulă Laplace permite să se găsească probabilitatea ca evenimentul A în n studiile independente să aibă loc cel puțin și nu mai mult decât o dată.
Formula integrală Laplace. În cazul în care probabilitatea p a evenimentului A în fiecare proces este constant și diferit de 0 și 1, atunci probabilitatea ca un eveniment A în studii independente n vin cel puțin și în cele mai multe ori, pentru un număr suficient de mare n este aproximativ egal cu
Este funcția Laplace, (2.5)
Atunci când formula (2.4) dă, ca regulă, o eroare de calcul al probabilității care este satisfăcătoare pentru practică.
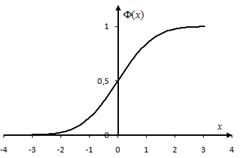
Valorile funcției pot fi găsite în Tabelul B.2 al cererii. Graficul este prezentat în Figura 2.3. Afișăm proprietățile funcției Laplace.
1. Funcția este ciudată, adică ..
2. Funcția crește în mod monoton, cu (practic se poate presupune că deja la).
Exemplul 2.4. În unele zone, din 100 de familii, 80 au un frigider. Care este probabilitatea ca între 300 și 360 de familii din cei 400 chestionați să aibă frigidere?
Un bun exemplu ar fi tehnic
Soluția. Aplicăm formula integrală Laplace (în primul rând, definim prin formulele (2.6)
Mai mult, folosind formula (2.4), luând în considerare proprietățile funcției # 934; (x), obținem:
(Din tabelul B.2 din anexa B).
Luați în considerare consecința formulei integrale Laplace.
Corolar. Dacă probabilitatea p de apariție a evenimentului A în fiecare test este constantă și este diferită de 0 și 1, atunci pentru un număr suficient de mare de studii independente, probabilitatea următoarelor evenimente este determinată de formule:
a) frecvența relativă a evenimentului A este între a și b:
b) frecvența relativă a evenimentului A diferă de probabilitatea sa de nu mai mult de magnitudine (în valoare absolută):
Atunci când și formulele Laplace dau o eroare satisfăcătoare pentru calculul practic al probabilității. Dacă n este de aceeași ordine cu 1 / n pentru n mare, sau. Un rezultat mai precis dă formula Poisson
2.1. Cât timp durează părțile pentru a se potrivi numărul cel mai probabil de părți egale cu 50, în cazul în care probabilitatea ca o parte luată la întâmplare va fi defect, este de 0,1?