Elementul algebrului sigma va fi numit un eveniment aleatoriu.
Grupul de evenimente complete
Un grup complet de evenimente este un grup complet de subseturi, fiecare dintre acestea fiind un eveniment. Se spune că evenimentele unui grup complet sunt o împărțire a spațiului de rezultate elementare.
Fie A o algebră. Funcție . maparea algebrei în setul de numere reale
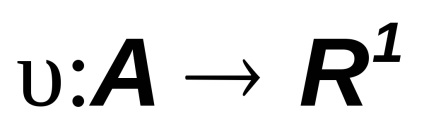
se spune că este aditiv finit dacă pentru orice set finit de evenimente pereche incompatibile
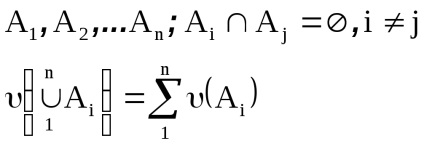
Fie F o algebră sau o algebră sigmatică. funcție
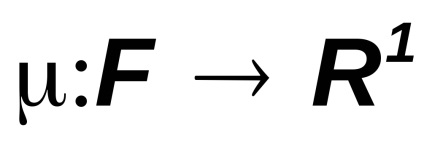
se spune că este aditiv în contracție dacă este aditiv finit și pentru orice set numărare de evenimente pereche incompatibile
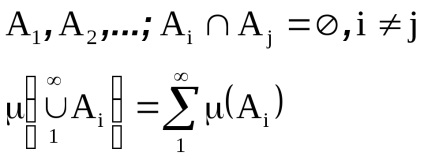
O măsură este o funcție de aditivare contradictorie non-negativă definită pe o condiție de satisfacere sigma-algebră
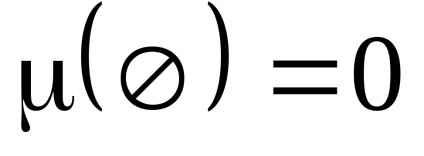
măsură

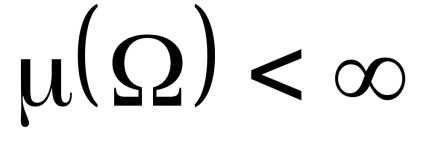
Probabilitatea (măsura de probabilitate) a lui P este o măsură de acest fel. că
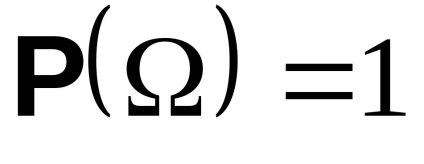
De acum înainte, vom opri măsurarea probabilității în procente și vom începe să o măsuram cu numere reale de la 0 la 1.
Când scrieți P, imaginați-vă mereu ce spațiu de rezultate elementare și sigma-algebră se înțeleg. Apoi puteți evita multe greșeli
Desemnarea P (probabilitate) pentru probabilitate este standard, nu trebuie să uităm că în sine (fără definirea spațiului de rezultate elementare și sigma-algebra) probabilitatea nu este definită.

se numește probabilitatea evenimentului A
Spațiul de probabilitate
Un spațiu de probabilitate este o colecție de trei obiecte - spațiul de rezultate elementare, sigma-algebra evenimentelor și probabilitatea.
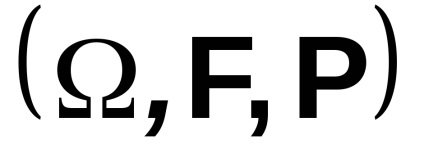
Acesta este modelul matematic al unui fenomen sau obiect aleatoriu.
Paradoxul definirii unui spațiu de probabilitate
Să ne întoarcem la formularea inițială a problemei teoriei probabilității. Scopul nostru a fost de a crea un model matematic al unui fenomen aleatoriu, ceea ce ar contribui la cuantificarea probabilității de evenimente aleatoare. În același timp, pentru a construi un spațiu de probabilitate, este necesar să se precizeze probabilitatea, adică pare să fie exact ceea ce căutăm (?).
Rezoluția acestui paradox este că, pentru o definiție completă a probabilității ca o funcție a tuturor elementelor F, este de obicei suficient pentru a defini doar pe unele dintre evenimentele din F, probabilitatea pe care le putem identifica cu ușurință și apoi, profitând de aditivitate sale numărabil, calculată pe orice element al lui F.
Evenimente independente
Un concept important al teoriei probabilității este independența.
Evenimentele A și B se consideră a fi independente dacă
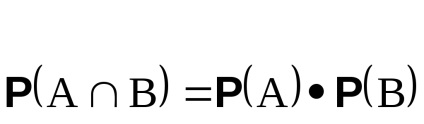
și anume Probabilitatea realizării simultane a acestor evenimente este egală cu produsul probabilităților lor.
Evenimentele dintr-un set numeric sau finit se spune că sunt independente în perechi, dacă o pereche de ele este o pereche de evenimente independente
Evenimentele dintr-un set numeric sau finit sunt numite independente în agregat. dacă probabilitatea implementării simultane a oricărui subset finit este egală cu produsul probabilităților evenimentelor din acest subset.
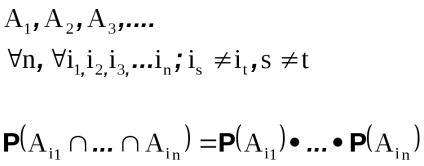
Este clar că evenimentele independente din agregat sunt independente și pereche. Reversul nu este adevărat.
Probabilitatea condiționată a evenimentului A, cu condiția apariției evenimentului B, este cantitatea
Probabilitatea condiționată este, pentru moment, determinată numai pentru evenimentele B ale căror probabilități nu sunt zero.
Dacă evenimentele A și B sunt independente, atunci
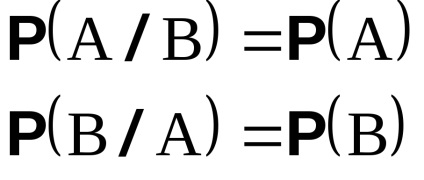
Proprietăți și teoreme
Cele mai simple proprietăți de probabilitate
Rezultă din faptul că A și non-A sunt opuse și proprietățile aditivității finite a probabilității
Probabilitatea evenimentului opus
Rezultă din faptul că evenimentele imposibile și autentice sunt opuse
Probabilitatea unui eveniment imposibil
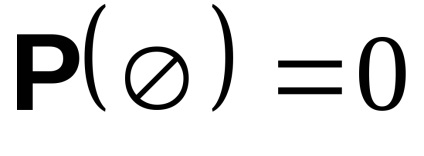
Rezultă de aici. că
și în acest caz
Rezultă din faptul că orice eveniment este conținut în spațiul rezultatelor elementare