Definiția. Fie variabilele aleatoare ξ1. £ 2. ..., ξn sunt independente și fiecare dintre ele are o distribuție normală standard N (0, 1). Se spune că variabila aleatoare χ 2n este definită ca
,
are o distribuție chi-pătrat cu grade de libertate.
Pentru a desemna această distribuție, expresia χ 2n este, de asemenea, utilizată de obicei.
Este clar că χ 2n (pentru orice η> 1) cu probabilitatea 1 ia valori pozitive. Funcția de densitate χ 2n la punctul x (x> 0) este egală cu
.
unde r (-) - este o funcție gamma. În practică, această densitate de distribuție este folosită rar direct.
Funcțiile densității distribuției chi-patrate cu un număr diferit de grade de libertate sunt prezentate mai jos.
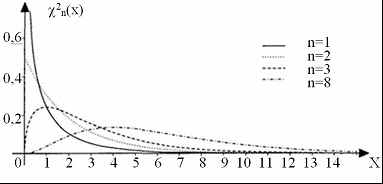
Fig. Funcția de distribuție este un chi-pătrat cu un număr diferit de grade de libertate n
Previziunea matematică și varianța variabilei aleatoare χ 2n sunt egale cu:
,
.
diverse tabele compilate pentru aleatoare 2n χ variabilă. Cel mai adesea, ele conțin valorile p-cuantila variabilelor aleatoare χ 2n. n = 1, 2 m (dacă probabilitatea este exprimată ca procentaj, denumit puncte de interes și, respectiv, vorbim despre tabelele de puncte procentuale). Argumentul p, 0<р<1, при этом пробегает тот или иной набор значений.