§ 1. Primul semn al egalității de triunghiuri.
1. Desenați triunghiul ABC. Dați definiția unui triunghi.
2. a) Notați toate simbolurile posibile pentru acest triunghi.
b) Specificați: partea care se află în raport cu unghiul C; unghiul care se află pe partea SM; unghiurile adiacente la nivelul UE; unghiul dintre laturile UE și EM (Fig.1.1).
c) Măsurați partea mai mică a acestui triunghi și unghiul mai mare și înregistrați rezultatul măsurătorii (Fig.1.1).
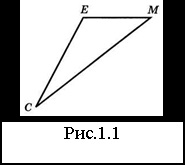

a) # 8710; CEM _____________________;
b) Latura ____ se situează opus unghiului C; pe partea SM se află __________; În partea UE sunt colțurile _______; între părțile UE și EM - colțul ______;
c) EM = _____ cm; # 8710; CEM = _______.
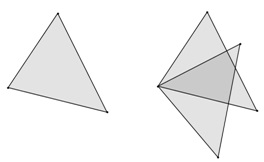
3. Gasiti triunghiuri egale, indicati elementele lor egale (Fig.1.2, Fig.1.3, Fig.1.4).
b) Utilizarea unui film transparent.
Pune-o pe el # 8710; ABC. cerc, apoi aplicați filmul la # 8710; A1B1C1. Pentru facilitarea alinierii, prindeți filmul la A1 cu butonul (figura 1.6).
3. Închideți câte perechi de elemente egale sunt suficiente pentru egalitatea triunghiurilor? Denumiți aceste elemente. Menționați teorema.
Atunci când triunghiul ABC este suprapus pe triunghi, MCN al laturii AB este aliniat cu partea MC. Partea laterală a difuzorului se află pe partea laterală a MN.
Partea forțelor armate a fost aliniată cu partea SC? Explicați răspunsul.
Soluția. Întrucât părțile AB și UA au fost aliniate părților _____. atunci punctele B și C coincid cu punctele ______, respectiv. În consecință, capetele segmentelor BC și ____ sunt aliniate și, prin urmare, segmentele BC și CN ______.
1. Citiți instrucțiunea teoremei primului semn al triunghiurilor, în manuale.
2. Notați condiția teoremei.
3. Faceți un desen.
4. În textul manualului citiți și analizați dovezile teoremei.
5. Scrieți ideea de dovadă în notebook:
Răspundeți la întrebări:
Ø De ce există un triunghi A1B1C1 egal cu triunghiul ABC?
Ø Ce inseamna ca triunghiul A1B2C2 este egal cu triunghiul ABC?
Ø De ce punctul B2 coincide cu punctul B1?
De ce fasciculul A1C2 coincide cu raza A1C1?
Ø De ce punctul C2 coincide cu punctul C1?
6. Completați spațiile în formularea și dovada primului test pentru egalitatea de triunghiuri.
Teorema. Dacă două laturi și unghiul dintre ele dintr-un triunghi sunt egale cu _____________________________ unui alt triunghi, atunci astfel de triunghiuri ___________;
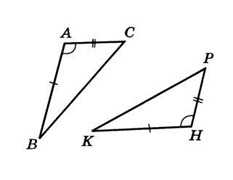
Dovedeste-o. # 8710; ABC = ________;
1) Prin ipoteza teoremeiÐA =ÐH. Prin urmare, triunghiul ABC
pot fi impuse ___________________ astfel încât vârful A
va fi combinată cu vârful H. Dar laturile AB și AC vor fi aplicate respectiv la razele NK și _______;
2) Prin condiția AB = _____. AC = ______, prin urmare, partea AB va fi aliniată cu partea ___________. și partea laterală a difuzorului - cu partea ______. în special, punctele B și ___ sunt combinate. C și ____.
Prin urmare, părțile _________________________;
3) Deci, triunghiurile ABC și NKR se unesc complet, deci sunt ___________. Teorema este dovedită.
Rezolvați problemele pe cale orală în conformitate cu desenele:
a) Descoperiți că triunghiurile din figură sunt egale și scrieți această egalitate (figura 1.8).
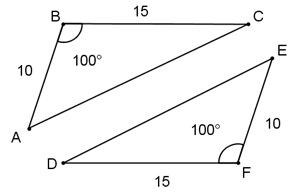

c) Găsiți CD-ul (figura 1.10).

Rezolvați probleme pe desenele pregătite: