Mai jos sunt câteva exemple de construcții în proiecții izometrice și dimetrice dreptunghiulare.
I. Proiecția sferei. În Fig. 473 de mai sus este imaginea unei sfere în proiecții izometrice și dimetrice.
În ambele cazuri sfera este prezentată cu o decupare de o parte opt. Cercurile reprezentând un contur al proiecției au fost trase: pentru o proiecție izometrică cu o rază egală cu
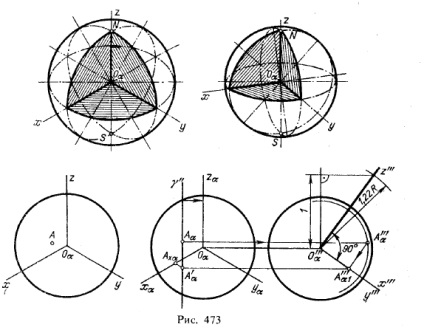
1.22R, pentru o proiecție dimetrică cu o rază de 1,06R, unde R este raza sferei. Elipsele în ambele cazuri corespund secțiunilor ecuatoriale și celor două secțiuni transversale.
Figura 473 de mai jos stânga, având în vedere domeniul de aplicare a imaginii într-o vedere izometrica; pe partea vizibilă a sferei este dat punctul A. La dreapta este prezentată construcția proiecțiilor secundare A'α (vezi figura 449) și trei niveluri de coordonate polyline A'α Ahα Oα Aa. care face posibilă determinarea coordonatelor dreptunghiulare ale punctului A în spațiu. Construcții făcut pe presupunerea că planul de proiecție izometrică ocupă o poziție frontală, și că ravnonaklonennyu la aceasta axa x, y, z coordonatele rectangulare proiectate nu numai pe acest plan, ci și pe plan suplimentar π3 profilate. Obținem un sistem de planuri de proiecție α, π3 și proiecții Aα și A '"α ale punctului A dat, unde A'" α este obținut prin intermediul secțiunii transversale a sferei π. γ. Proiecția secundară a punctului A este reprezentată și de două proiecții: A "" α1 și A'α
2. Linii de intersecție a unui cilindru și a unui con cu un plan. Figurile 474 și 475 prezintă construcția în proiecția izometrică a liniilor de intersecție a cilindrului și a conului prin planuri de proiectare frontală. În cazurile analizate, liniile de intersecție sunt elipse.
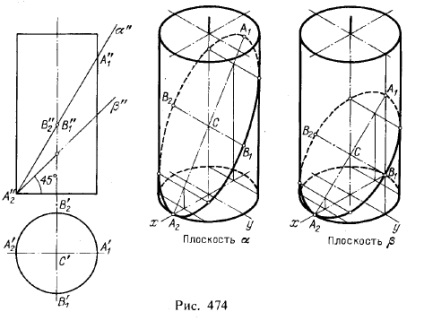
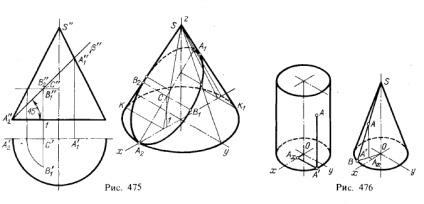
În primul rând, pe baza desenului, trasăm de-a lungul coordonatelor punctelor A1 și A2 liniile de pante ale planurilor α și β. Pentru construirea punctelor de elipsă luăm avioanele auxiliare secante: pentru cilindru - paralel cu generatoarele sale și planul yOz, pentru con -
1) Construcția se realizează în coeficienții de denaturare redusă.
Trecând prin vertexul său paralel cu axa y. Aceste planuri sunt date de liniile lor paralele cu axa y, pe planurile bazei cilindrului și ale conului.
Cu această alegere a planurilor auxiliare, liniile drepte de-a lungul cărora se intersectează planurile α și β sunt obținute paralel cu axa γ. Punctele elipsei se obțin la intersecția acestor linii cu generatoarele cilindrului și conului.
În primul rând, ar trebui să găsiți astfel de puncte caracteristice, așa cum sunt marcate în desene cu literele A1. A2. B1 și B2. și proiecția izometrică obținută pe liniile schițate. Axa semimajor a elipsei obținută în secțiune este egală cu C'B'1. își păstrează și valoarea în proiecția izometrică (C'B'1 = CB1). Dar valoarea axei sale mici pentru o elipsă într-o proiecție izometrică păstrează segmentul B1 B2 numai pentru m. β, adică cu unghiul de înclinare al acestui plan, indicat în figură, egal cu 45 °.
Într-adevăr, în acest caz, segmentul B1 B2, care este paralel cu axa y, rămâne în proiecția izometrică perpendiculară pe A1 A2. în consecință, segmentele A1 A2 și B1 B2 își păstrează valoarea axelor de elipse. În cazul unei înclinații diferite a planului, așa cum se arată pe cilindru pentru pl. α, segmentele A1 A2 și B1 B2 în proiecția izometrică nu sunt axele elipsei, ci doar diametrele conjugate ale acestora.
3. Construcția segmentelor de coordonate pentru un punct definit pe suprafața unui cilindru și un con de rotație în proiecția axonometrică. În Fig. 476 oferă exemple pentru un cilindru și un con în proiecție izometrică. În toate cazurile, originea este luată în centrul bazei (punctul O).
O linie dreaptă paralelă cu axa z este trasă prin punctul A pe cilindru, iar din proiecția secundară A 'se trasează o linie dreaptă paralelă cu axa y până când se intersectează axa x. Segmentele 0Ax. Axele A 'și A'A ne permit să determinăm coordonatele punctului A dintr-un sistem dat de axe de coordonate.
Prin intermediul unui punct A pe con, este construit un generator și este construită o proiecție secundară (OB) a acestui generator. Desenând o perpendiculară de la punctul A la intersecția cu OB, obținem o proiecție secundară a punctului A. Mai departe este clar din desen.
În Fig. 477 prezintă construcția segmentelor de coordonate pentru un punct definit pe suprafața unui con de trunchi de rotație într-o proiecție izometrică (figura 411, a). Să presupunem că avem o secțiune a conului printr-un plan care trece prin axă
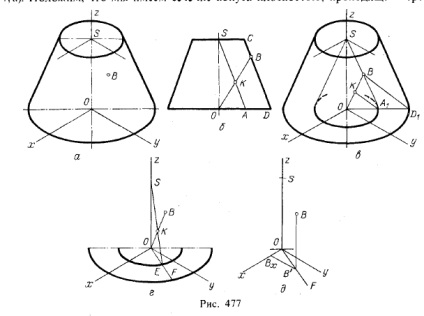
con și punctul B (figura 477.6). În trapezoidul rezultat, linia SA || CD-ul și linia OB traversând-o la punctul K. Ne simțim bine. KB = OA. AD. Dar această proporție va rămâne în proiecția izometrică. Construim un con cu vârf la punctul S și cu un generator paralel cu generatorul conului trunchiat (figura 477, c). De la
purtând OA1. A1 D1 repetă raportul OA. AD, conținut în proporția de mai sus. Acum putem obține punctul K pe OB în Fig. 477, c. Generator, trasată prin punctele S și E, determină punctul K (Fig. 477 g) și proiecția formarea OF, care este punctul B. Din aceasta vom putea primi o proeminență B secundar „(Fig. 477, etc.) și coordonate segmentele BB ', B'Bx și OBx. coordonatele z, y și x.
Această construcție este dată în cazul în care conul trunchiat nu poate fi completat la maxim. Dacă puteți termina construcția, atunci se execută construcția, așa cum se arată pentru con în Fig. 477.6.
4. Exemple de construcție a liniilor de intersecție a suprafețelor cilindrice și conice de rotație între ele. Liniile de intersecție sunt construite de puncte; aceste puncte se găsesc fie prin coordonatele lor luate din proiecții ortogonale, fie prin metoda planurilor auxiliare secante direct în proiecții axonometrice. Acesta din urmă este prezentat în Fig. 478, a -
Planurile auxiliare secante intersectează aceste cilindri și conuri de-a lungul liniilor de generare. În Fig. 478, iar axele cilindrilor se intersectează, în fig. b) încrucișarea. Dacă în Fig. a) punctele A și A1 au fost determinate folosind un plan secant care trece prin axele ambelor cilindri, apoi în Fig. b) este necesar să se ia în considerare deplasarea
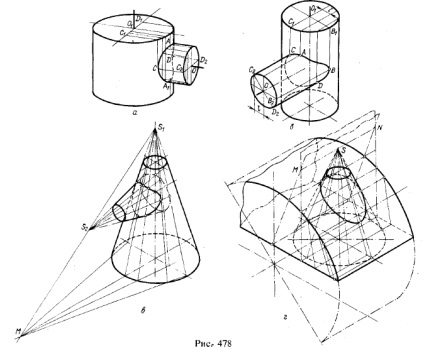
l 1). În Fig. 478, în planurile de tăiere trec prin linia S1S2. iar urmele lor pe planul bazei conului cu vârful S1 trec prin traiectoria liniei S1 S2 pe acest plan. În Fig. 478, r a planului trece prin linia MN trasată prin vârful conului - punctul S - paralel cu generatorul cilindrului.
1) Marcarea punctelor cu litere se face doar pentru explicații.
5. Construirea punctelor de tangență a cercului - o contură a proiecției sferei - cu o elipsă - proiecția cercului obținut pe sferă când se intersectează cu un plan. În Fig. 479, iar sfera este tăiată cu trei planuri - profilul (γ), orizontal (δ) și proeminent (β) este prezentat. Conform acestui desen, o proiecție izometrică (figura 479.6) este construită în coeficienții de distorsiune redusă. Elipsa m este construită așa cum se arată în Fig. 469, iar elipsa n - ca în Fig. 465. Proiecția sferei este dată de un contur - un cerc cu o rază egală cu 1,22R. Acest cerc atinge elipsa m la punctul K, elipsa n - la punctul L.
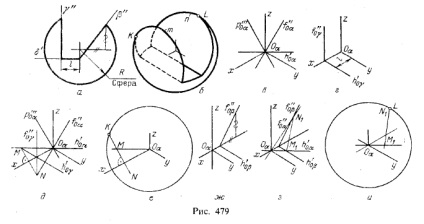
Să considerăm, ca punct găsită K. Se obține pe circumferință - .. Schița sferă de proiecție, adică în planul vedere în perspectivă (α), și în același timp, pe elipsă m adică, mp ... γ traversând sfera. Dar, în cazul în care punctul aparține simultan două planuri, apoi aparține linia de intersecție a acestor avioane.
Planul izometric de proiecție este cunoscut a fi înclinat în mod egal la π1. π2 și π3. Triunghiul de urme ale acestui plan este echilateral (vezi figura 457). Referindu-se la pl. α la punctul Oα. adică la începutul axelor și la centrul sferei, vom suferi poziția liniilor indicate în Fig. 479, c.
Pl. γ în sistemul acelorași axe este prezentat în șine, așa cum se arată în Fig. 479, g. Compatibil cu Fig. c) și d) și construi linia de intersecție a avioanelor a și γ (Figura 479, e). linia MN trece prin punctul M de intersecție a urmelor orizontale urmând p paralel „„0α deoarece y || π3 (în care P.“ '0α ⊥Oα X. Prin urmare, MN⊥Oα x).
Acum rămâne să găsim punctul K la intersecția liniei MN cu cercul - proiecția izometrică a sferei (Fig.479, e).
Pentru a determina poziția punctului L (vezi figura 479, b), este necesar să se prezinte un plan de proiectare frontală în sistemul axelor izometrice. β (Fig. 479 g) A, și apoi găsiți linia de intersecție a avioanelor a și β (Fig. 479, s), această linie trece prin punctul de intersecție M1 și h'0α h'0β urme și prin punctul de intersecție N1 piese f " 0β și f "0α. Punctul dorit L este obținut la intersecția liniei M1 N1 cu cercul - proiecția izometrică a sferei (Fig.479, i).