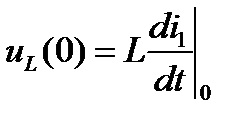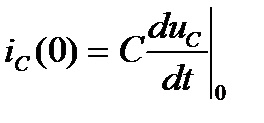Constantele de integrare în expresiile pentru constituenții liberi, se calculează prin substituirea condițiile inițiale sunt cunoscute în expresiile pentru funcția dorită și ei (n - 1) derivate la momentul t = 0+ (n - numărul de rădăcini ale ecuației caracteristice).
În cel mai general caz, când ecuația caracteristică are
n rădăcini și soluția pentru curentul sau tensiunea tranzitorie este scrisă sub formă
. pentru a găsi constantele de integrare A1. A2, ...... Este necesar să se compună un sistem de n ecuații cu următoarea formă
În aceste ecuații, valorile componentelor forțate pentru
t = 0+.
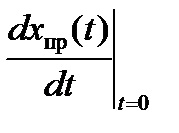
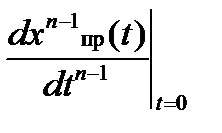
Dacă problema implică un proces tranzitoriu în circuitul DC, atunci. și toate derivatele sunt zero.
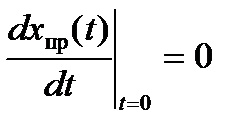
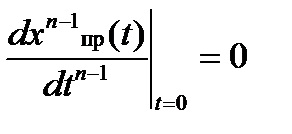
În circuitul de curent sinusoidal, componentele forțate variază de asemenea în funcție de legea sinusoidală. Primul derivat pentru ele este dat de expresie.
Pentru timpul t = 0.
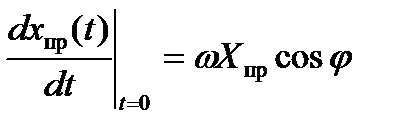
Tabelul 2.6 prezintă expresiile pentru curenții sau tensiunile tranzitorii și pentru primii derivați ai acestora în cazul unui proces tranzitoriu într-un circuit de curent continuu.
Ecuațiile pentru calcularea constantele de integrare sunt prezentate în ultima coloană a tabelului, acestea pot fi obținute, în cazul în care valoarea expresiei a tranziției și primul substitut t derivat = 0.
Tabelul 2.6 - Ecuații pentru calcularea constantelor de integrare
Expresii pentru curenții și tensiunile tranzitorii
Condițiile inițiale necesare
Expresii primelor derivați pentru curenții și tensiunile tranzitorii utilizate pentru calcularea constantelor de integrare
Ecuații pentru calcularea constantelor de integrare (pentru un proces tranzitoriu într-un circuit cu curent constant)
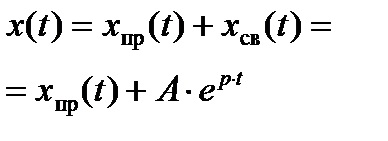
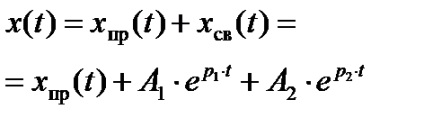
;
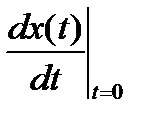
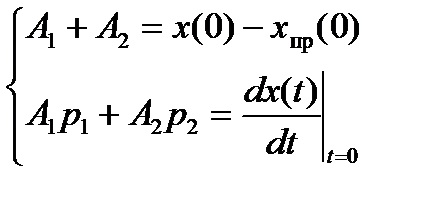
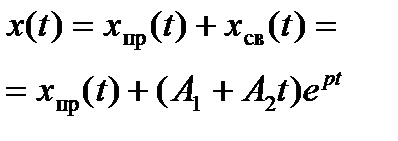
;
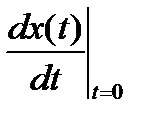
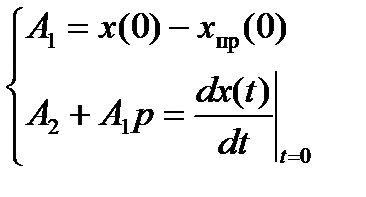
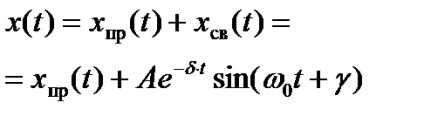
;
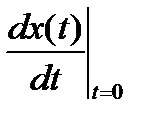
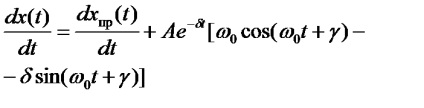
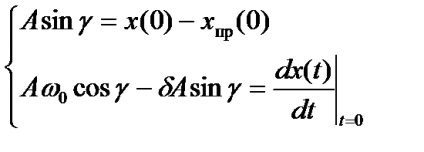
Pentru a determina constantele de integrare în conformitate cu formulele din tabelul 2.6, este necesar să se calculeze mai întâi condițiile inițiale.
Condițiile inițiale sunt valorile curenților, tensiunilor și derivaților acestora în momentul inițial al procesului tranzitoriu, la.
Condițiile inițiale sunt împărțite în mod independent și dependent.
Condițiile inițiale independente sunt valorile curenților elementelor inductive și ale tensiunilor elementelor capacitive pentru timp
Condițiile inițiale independente sunt determinate de legile de comutare. ; .
Acestea pot fi zero și nonzero.
Condițiile inițiale dependente sunt valorile tuturor celorlalte curenți, tensiuni și derivate de timp ale curenților și tensiunilor pentru timp. Condițiile inițiale dependente sunt definite:
- după ce se calculează condițiile inițiale independente;
- din ecuațiile în conformitate cu legile lui Kirchhoff pentru schema post-comutație înregistrată pentru timp.
Numărul de condiții inițiale care trebuie calculate este egal cu numărul de constante de integrare din expresia pentru valoarea de tranziție. După cum se arată în Tabelul 2.6, dacă ecuația caracteristică are o rădăcină și o exprimare liberă a curentului sau a tensiunii cuprinde una constantă necunoscută de integrare pentru a determina nevoie doar pentru a calcula o valoare inițială condiție a funcției. Dacă constantele de integrare necunoscute sunt două, atunci se calculează două condiții inițiale pentru determinarea lor: valoarea funcției însăși și a primei sale derivate
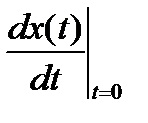
E = 100 V, R1 = 10 Ω, R2 = 10 Ω,
R3 = 10 Ohm. L = 0,1 H
În primul rând, găsim o condiție inițială independentă. pentru acest sistem este
curent. deoarece aceasta este curentul prin inductanță. Conform primei legi de comutare, aceasta va fi egală cu curentul prin aceeași inductanță în ultimul moment înainte de comutare.
Înainte de comutarea în circuit (Figura 2.36), un DC
Acest curent este constant și de timp
nu depinde, deci pentru timp
Conform primei legi de comutare
Valorile inițiale necunoscute ale curenților și curenților pentru inductanță sunt condițiile inițiale dependente.
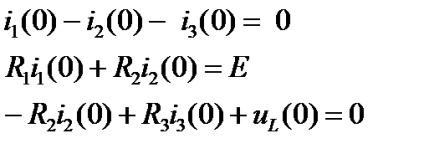
Sunt necunoscute în aceste ecuații. Ele pot fi găsite prin rezolvarea sistemului compilat de ecuații prin orice metodă din Mathcad sau manual, de exemplu, folosind substituția.
Din prima ecuație îl exprimăm și o substituim în cea de-a doua ecuație.
Exemplul 2 (Figura 2.37)
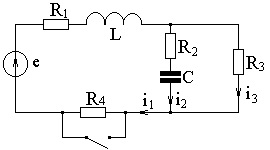
E = 100 V; = 10 Ohm;
= 20 Ohm; L = 0,05 H; C = 250 uF.
Din circuitul înainte de comutare găsim condiții inițiale independente (curent inductiv și tensiune de elemente capacitive pentru instantaneu t = 0-). Deoarece ramura cu un element capacitiv la E = const nici un curent, atunci: i1 (0) = i3 (0) = E / (R1 + R3 + R4) și i1 (0) = 100 / (10 + 10 + 20) = 2,5 A,
Pentru a determina condițiile inițiale dependente, scriem ecuațiile în conformitate cu legile lui Kirchhoff pentru circuit după comutare pentru momentul t = 0+:
.
Substituind condițiile inițiale independente de mai sus i1 (0) și uC (0) în aceste ecuații, găsim: A; A; B.
Derivatul curentului prin inductanță se găsește din formula