Pentru fiecare matrice pătrată A se introduce numărul | A |, care se numește determinantul său. Uneori este indicat și printr-o literă Δ.
Acest concept este important pentru rezolvarea unui număr de probleme practice. Definiți-o prin metoda de calcul.
Pentru o matrice A de ordinul întâi, determinantul ei este elementul său unic | A | = Δ1 = a11.
Pentru o matrice A de ordinul doi, determinantul său este un număr care este calculat prin formula | A | = Δ2 = a11 * a22 - a21 * a12
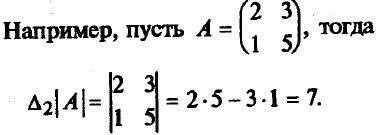
Pentru o matrice A de ordinul trei, determinantul ei este un număr care este calculat prin formula
Acesta reprezintă o sumă algebrică formată din 6 termeni, fiecare conținând exact un element din fiecare rând și din fiecare coloană a matricei. Pentru a reaminti formula determinantă, se obișnuiește să se folosească așa-numita regulă de triunghiuri sau regulă Sarrus (Figura 6.1).

Figura 6.1 - Regula triunghiulare
În Figura 6.1, diagrama din stânga arată modul de selectare a elementelor pentru semnul plus - ele se află pe diagonala principală și la vârfurile triunghiurilor isoscel, ale căror baze sunt paralele cu ele. Schema din stânga este folosită pentru termenii cu semnul minus; pe el în locul diagonalei principale se ia așa-numita garanție.
Determinanții ordinelor superioare sunt calculați recursiv, adică determinantul ordinii a patra prin determinantul ordinii a treia, determinantul ordinii a cincea prin determinantul ordinii a patra, etc. Pentru a descrie această metodă, este necesar să se introducă conceptele de completare minoră și algebrică a elementului matricei (am observat imediat că metoda în sine, care va fi luată în considerare mai jos, este de asemenea potrivită pentru determinanții ordinelor a treia și a doua).
Minusul Mij al elementului aij al matricei n-ordin este determinantul matricei de ordine (n-1) obținute din matricea A prin ștergerea rândului i și coloanei j.
Fiecare matrice de ordine n-a are n 2 minori (n-1).
Un complement algebric Aij al elementului aij al unei matrice n-a ordinii este minorul său luat cu semnul (-1) (i + j):
Din definiția rezultă că Aij = Mij. dacă suma numerelor rândului și coloanei este uniformă și Aij = -Mij. dacă este ciudat.
De exemplu, dacă
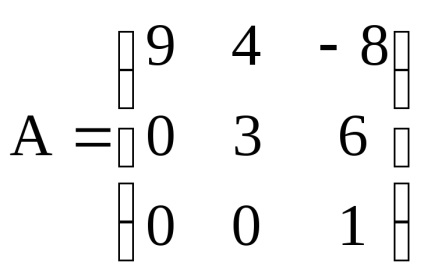
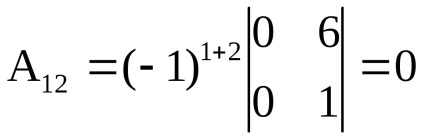
Metoda de calcul a determinantului este după cum urmează: determinantul unei matrici pătrate este egal cu suma produselor elementelor din orice rând (coloană) prin complementare lor algebrice:
(extinderea pe elementele liniei i-a;
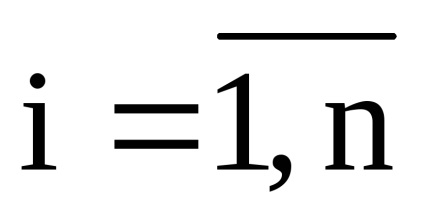
(extinderea elementelor coloanei j;
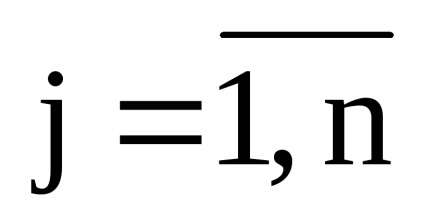

Observăm că în cazul general, determinantul unei matrice triunghiulare este egal cu produsul elementelor principalei diagonale.
Să formulăm proprietățile de bază ale factorilor determinanți.
1. Dacă un rând sau o coloană a matricei constă doar din zerouri, atunci determinantul este 0 (rezultă din metoda de calcul).
2. În cazul în care toate elementele din orice rând (coloană) a matricei se înmulțește cu același număr, atunci determinant său se înmulțește cu acest număr (după cum rezultă din metoda de calcul - calculul cofactori factor comun nu este afectat, iar toți ceilalți termeni sunt multiplicate acesta este numărul).
Notă: pentru semnul determinantului, este posibil să se facă un factor comun doar pentru rând sau coloană (spre deosebire de matricea, dincolo de care factorul comun al tuturor elementelor sale poate fi considerat ca un semn). De exemplu, dar
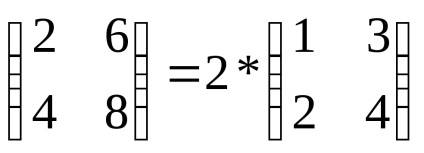
3. Atunci când matricea este transpusă, determinantul său nu se modifică: | A | T | = | A | (nu vom face dovada).
4. Atunci când două rânduri (coloane) ale unei matrice sunt schimbate, modificările determinante semnează contrariul.
Pentru a dovedi această proprietate inițial presupune că au schimbat cele două rânduri adiacente ale matricei: i-i și (i + 1) th. Pentru calcularea determinantului matricei inițiale este fezabilă pentru descompunerea rândul i-lea și pentru determinantul noii matrice (rândul-permutate) - la (i + 1) th (adică este același și anume element, prin potrivire elementul). Apoi, calcularea celui de al doilea factor determinant, fiecare plus algebrică va avea semnul opus ca (-1) va fi construit nu în gradul de (i + j) și în gradul de (i + 1 + j), dar altfel nu va diferi formula. Astfel, semnul determinantului se schimbă în contrariul.
Acum, să presupunem că nu sunt rearanjate liniile adiacente, ci cele două linii arbitrare, de exemplu, i-th și (i + t) -th. Această permutare poate fi reprezentat ca un natstrok smescheniei secvențial th rând în jos, și (i + t) rândul -lea - la (t-1) aliniaza 1. Aceasta va schimba semnul determinantului (t + t- 1) = numărul 2t- 1 ori, adică un număr ciudat de ori. În consecință, în cele din urmă, se va inversa.
Un asemenea raționament poate fi modificat pentru coloane.
5. Dacă matricea conține două rânduri identice (coloane), determinantul său este 0.
De fapt, dacă aceleași rânduri (coloane) sunt rearanjate, atunci se va obține aceeași matrice cu aceiași determinanți. Pe de altă parte, în funcție de proprietatea anterioară, trebuie să schimbe semnul, adică = -ΔΔ = 0.
6. Dacă elementele a două rânduri (coloane) ale matricei sunt proporționale, atunci determinantul este 0.
Această proprietate se bazează pe proprietatea anterioară și pentru scoaterea colțarul factor comun (după îndepărtarea coeficientului de proporționalitate între paranteze în matricea va avea aceleași rânduri sau coloane, și ca urmare, acest coeficient va fi înmulțit cu zero).
7. Suma produselor elementelor din orice rând (coloană) a matricei prin complementul algebric al elementelor unui alt rând (coloană) a aceleiași matrici este întotdeauna 0:
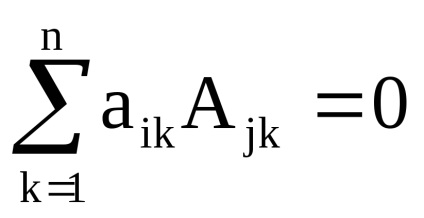
Pentru a demonstra această proprietate, este suficient să înlocuiți linia j cu linia i în matricea A. În matricea rezultată vor exista două rânduri identice, deci determinantul său este 0. Pe de altă parte, poate fi calculat prin extinderea elementelor din rândul jth:
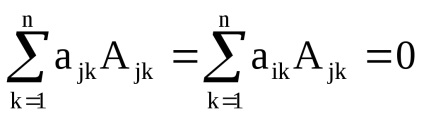
8. Factorul determinant al matricei nu se modifică în cazul elementelor dintr-un rând sau dintr-o coloană dintr-o matrice pentru a adăuga elemente ale altui rând (coloană) înmulțit cu același număr.
De fapt, să se adauge elementele liniei j, înmulțite cu приба, la elementele rândului i. Apoi elementele noului rând i-i ia forma (aik + ajk, k). Calculam factorul determinant al noii matrici prin extinderea elementelor din rândul i (notați că complementările algebrice ale elementelor sale nu se vor schimba în acest caz):
Am obținut că acest determinant nu diferă de factorul determinant al matricei inițiale.
9. Factorul determinant al produsului matricelor este egal cu produsul determinanților lor: | AB | = | A | * | În (nu vom face dovada).
Proprietățile determinanților considerați mai sus sunt utilizate pentru a simplifica calculul acestora. De obicei, ei încearcă să transforme matricea într-o astfel de formă încât orice coloană sau linie să conțină cât mai multe zerouri posibil. După aceasta, determinantul poate fi găsit cu ușurință prin extinderea acestui rând sau coloană.


