Pentru a tăia roțile dințate
Coeficienții de polarizare sunt atribuite:
- creșterea rezistenței la încovoiere a dinților prin creșterea secțiunii lor periculoase în apropierea bazei;
- creșterea rezistenței de contact a dinților prin utilizarea unor secțiuni involute care sunt mai departe de cercul principal;
- alinierea alunecării maxime specifice;
- împiedica subcotarea roții mici din angrenaj;
- creșterea netedă a transmisiei prin extinderea liniei active de cuplare;
- asigurarea unei distanțe date interactive;
- furnizarea unei unelte cu două perechi în pol și în alte scopuri.
Calculul dimensiunilor geometrice ale pinioanelor
Datele inițiale pentru calcularea dimensiunilor sunt: numărul de dinți ai roților și. roată. unghiul profilului conturului original. coeficienții de deplasare și. coeficientul de înălțime al capului dentar și coeficientul de degajare radială.
Formula de determinare a unghiului de cuplare este dată aici fără nici o inferență, datorită volumului său
Din această formulă, în special, se poate observa că la angrenajul zero, unghiul de cuplare este egal cu unghiul profilului sculei. într-un transfer pozitiv. în transmisia negativă, totul este inversat, adică și, respectiv.
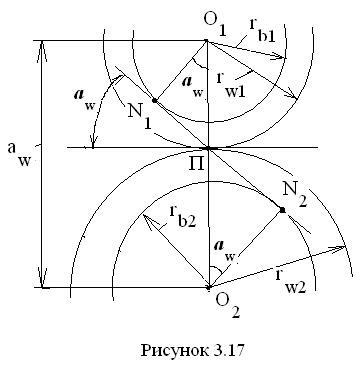
Pentru a deduce formulele, ne îndreptăm către Fig. 3.17, care prezintă elementele necesare de implicare. Linia de angajare N1 N2 formează unghiul de angajare W cu o comună tangentă la cercurile inițiale ale raziilor și. legate unul de altul în pol # 928 ;. Diminuarea perpendicularele din centrele O1 și O2 de roți pentru angajarea liniei, obținem cele două triunghiuri drepte N1 O1 și P 2O 2 P, cu unghiurile de la vârfurile O1 și O2. egal # 945; w. Din triunghi urmează N1 O1 P. din triunghiul N2O2P-. Deoarece există egalități. . și. de asemenea. . atunci obținem și. În loc de razele de cercuri împărțite și în aceste formule se pot introduce expresiile lor scrise mai devreme
După cum se poate vedea din figură, distanța interaxială este egală cu suma razei cercurilor inițiale, adică .. prin urmare
Produsul primilor doi termeni din această formulă se numește distanța interaxială divizibilă. Apare atunci când transmisia este făcută la zero, adică atunci când coeficientul total de deplasare este zero. În acest caz. iar cosinusul scade.